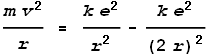The Structure of Protons and Neutrons

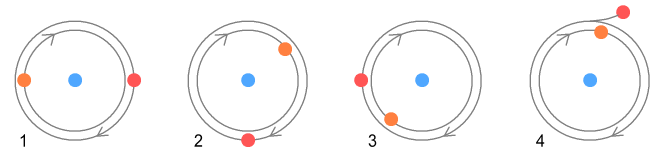
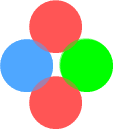
In this chapter we’ll look at protons and neutrons in more detail.

Basic layout of a proton

In the earlier chapter on nuclear forces I suggested a proton was made of two (positively charged) up-quarks orbiting a (negatively charged) down-quark. It looked like this:

Here the up-quarks are held in place by a simple combination of electrical and centrifugal forces. This layout has the important benefit that the orbiting up-quarks generate sine-wave electromagnetic signals that are 180 degrees out of phase and hence cancel each other. But it also has problems. One is stability: how can we guarantee the up quarks will stay in place and keep the structure from falling apart? The other is ‘quantum mechanical’: what could keep the up-quarks at a fixed distance when any number of orbits altitudes are possible?

In an earlier chapter on atomic orbits, similar problems were discussed regarding the layout of a helium atom and the orbit of its electrons. One possibility considered for helium was having its two electrons stay exactly opposite each other. This is very similar to our proton structure. But it failed for helium so how could it work for a proton? I’ll address each of these problems in turn.

Problem 1: Ejection from underneath

The first problem involves keeping the orbiting up quarks opposite each other. As pointed out in the atomic orbits chapter (in point 2), unless the electrons could be kept exactly opposite each other, there’s nothing to prevent one from dropping into a lower, and hence faster, orbit and moving underneath the other. In this case the problem is with the up-quarks rather than electrons as this diagram shows:

The above four frames show what happens when an up-quark enters a slightly lower orbit. Due to it being closer to the centre, the low-orbit quark (painted orange) moves faster and eventually works its way underneath the high-orbit quark (red). At this point the high-orbit quark is ejected and the proton’s structure destroyed.

A solution to this is to note that the centre quark can move. In the chapter on particle physics I speculated that up and down quarks are actually pions and muons respectively, and that muons are nine times lighter than pions. Drawn by the pull of the heavier up-quarks, the light-weight down-quark would easily manoeuvre to reposition itself in-between as this diagram shows:

If the situation were reversed, with the middle quark being 9-times heavier, this manoeuvre seems less likely. This may explain why up-quarks are able to orbit the down and not vice-versa.

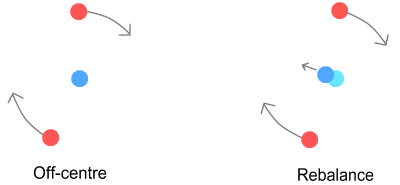
Problem 2: Sideways force imbalance

The next problem involves horizontal stability, namely that the promotional force from the down-quark will be double that of the retarding force from the opposing up-quark. As a result, the orbiting quarks would immediately spin away from the centre quark, thus destroying the proton. See the chapter on atomic orbits (in point 3) for a detailed description of the equivalent problem involving a negative hydrogen ion (a hydrogen atom with two electrons).

Fortunately there appears to be a solution for this also. Namely that the quarks have finite size. The centre down-quark wouldn’t stay motionless; rather, it would rotate in-sync with the orbital motion of the up-quarks. See diagram.

As a result the field lines that leave the down-quark already have a small forward component. This component reduces the velocity difference between the down and up quarks and hence reduces the promotional sideways force. Meanwhile the retarding sideways force between up-quarks stays the same. When the up-quark is at a high altitude this reduction will be minor and won’t stop the up-quark from spiralling outward. But when it’s at low altitude the reduction becomes significant. When the up-quarks orbit close enough, at some point the promotional sideways force become equal and opposite to the retarding sideways force and the two cancel.

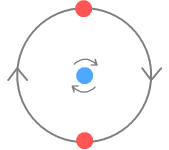
Problem 3: Vertical stability

With the up-quark orbiting at the proper altitude, we now have an equilibrium situation in which the horizontal sideways forces cancel and the electrostatic forces counterbalance the outward centrifugal force. This appears to be a happy situation for our stability-seeking proton. Alas there is another problem at hand: in order for the proton to be stable we need to show that it can self-correct for any orbital imperfections and external disturbances.

If the orbiting quarks were to increase or decrease their speed while maintaining the same altitude, the sideways forces would accordingly decrease or increase to correct the speed to its prior value. That’s all very well for the horizontal direction but how about increases or decreases in altitude, i.e. vertical stability? As has been already established, if the up-quark was too far away, the promotional sideways force would dominate and the up-quark would spiral away. When the up-quark is too low however the retarding sideways dominates and this would cause the up-quark to spiral downward. Obviously this is a problem because it’s not possible for the up-quarks to have exactly the right altitude.

Luckily there is a solution for this also. Refer to the second chapter on matter-energy conversion. There I suggested that subatomic particles could overlap each other. I will now suggest the same here, namely that the orbiting quarks will spiral down until touching then overlapping the down quark in the centre. It will look like this:

Much like the way a sinking hot air balloon comes to rest on the surface of a lake, as the up-quarks begin to overlap the down-quark they gain ‘buoyancy’. Or more correctly, the attractive force between positive and negative quarks reduces as the repulsive force between the two up-quarks continues to increase. At some point all forces balance and the altitude comes to rest. The proton now has a fixed diameter and is rotating at a set frequency. Seeing as the particles are now in direct contact and overlapping, this system appears very stable and is unlikely to be easily broken by collisions with other particles or electromagnetic waves. Nor will it come apart on its own. Indeed, this level of stability describes a proton quite well!

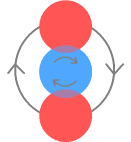
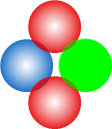
Structure of a Neutron

With the proton now described, it is an easy matter to extend that structure to a neutron. In the second chapter on nuclear forces I suggested the neutron consists of a proton with an electron by its side. I’ll keep the same structure here other than to do away with the fractional quarks charges for the reasons given in the particle physics chapter. The neutron will look like this:

The electron, shown in green, takes its place beside the centre down-quark and the up-quarks orbit both. The electron is drawn the same size as the other particles for the reasons given in the particle physics chapter. In this way it can overlap the up-quarks, thus making it stable. This would not be possible if electrons were much smaller as might be expected based on their mass. As with the proton, the particles are slightly overlapping. The neutron is shown face-on so all its particles are visible. Now here are 3D versions of the proton and neutron. The particles are drawn with “wireframes” so their rotation can be properly seen.

proton and neutron rotating

Neutron instability

Stable? Okay so a neutron isn’t completely stable. It’s well acknowledged that isolated neutrons will decay into a proton and electron – the neutron having a half-life of 10.3 minutes. If we look again at the neutron structure, both the down-quark and the electron occupy the same position within the structure. But the electron is extremely light. It is 206 and 815 times lighter than the down and up quarks respectively. With two heavy up-quarks in orbit around it, one might expect that the electron would have a hard time sitting still. Perhaps it will rattle about. Here’s an animation showing a possible electron wobble during the neutron rotation (again with wireframes, and two small dots to help see the wobble):

neutron with electron wobble

As the up-quarks spin in one direction, the electron perhaps bounces between them and perhaps rotates a bit. However this can’t continue indefinitely. This movement creates an instability in the electron which could cause it to become unstuck. On the other hand if the neutron was attached to a proton, such as within an atom’s nucleus, the electron would be held steady and there would be no instability.

Crunching the numbers

Up to this stage my description of nucleons has been only with words and diagrams. That’s fine for a general description but it would be nice to have more specific information about them, such as how far apart they are and how quickly they rotate. Knowing this requires knowing the diameter of a quark, which may also be the universal diameter of all sub-atomic particles. Unfortunately we don’t have this information but we can make some estimates.

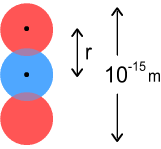
The measured diameter of a proton is considered to be about 10^-15 m. Assuming this contains exactly three quarks side-by-side, minimally overlapping, that makes the diameter of a quark 3.3x10^-16 m. Refer to the below diagram:

We wish to know the frequency and velocity of its rotation. Using simple force equations, the centrifugal force needs to match the net-inward electric force:

$\frac{m v^2}{r} = \frac{k e^2}{r^2}-\frac{k e^2}{(2 r)^2}$

Where m is the mass of an up-quark and r is the distance between two quarks – in this case their diameter. Substituting a value for m = 815 times an electrons mass, and solving for velocity and frequency we get:

Velocity = 2.6x10⁷ m/s
Frequency = 1.3x10²² Hz

Based on this the up-quarks are moving at around 9 percent the speed of light and rotating at 13 “Zettahertz”. In other words it’s all happening rather quickly! These numbers are of course very approximate because we don’t know the radius of either a quark or proton and are not taking into account the degree of overlap or complexities of the sideways force formulas, etc. Nonetheless it is reassuring to note that the calculated velocity does not require the quarks to move ridiculously fast, i.e. only a low percentage of light speed. In the case of a neutron there are two centre negative charges so we would expect the neutron to rotate faster; although not twice as fast because those charges are at an angle.

Problems with particle sizing

This neutron structure brings to light certain problems with earlier assumptions about particle sizes:

If the electron and down-quark are identical in both charge and size then it should be possible to construct a neutron using two down-quarks. Such a neutron would be very stable (no electron wobble) and common-place. It would also be highly noticeable due to it being 11 percent heavier than regular neutrons. Yet we don’t see any.
The down-quark and electron are very close together. From the diagram, it doesn’t look like the up-quarks would be able to hold them that close. We would expect the negative charges to force apart, at which point the neutron structure would be destroyed.

Based on this it would appear that our assumption about particle sizes might be wrong and that the electron needs to be smaller. But making the electron smaller would bring back the same problems with muon-poseltron decay interactions (see particle physics). It would also prevent a neutron from forming because the electron can’t float at a distance.

Therefore rather than reject the idea that these particles are a similar size, it’s best to look for another approach. The solution might be to distribute the particle’s charge unevenly. For example we could say the muon’s (down-quark’s) charge is concentrated mostly around the rim like this:

Here the shade of blue represents the concentration of charge, with dark blue representing more charge. We can also say an up-quark’s charge is distributed likewise but an electron’s charge is uniform. The neutron will look like this:

In this manner the electron and down-quark still repel but the neutron structure becomes possible due to the charged edges of the up-quarks being better able to grip the down-quark and electron. However, two down-quarks could not sit this close because of their charge concentration at the rim. This also helps explain how certain atomic nuclei structures could be stable. For example two neutrons could be close together, providing that the electron and down-quark are facing each other, rather than having two down-quarks in close contact. This charge-density would also allow a muon to force a poseltron apart.