Quantum Mechanics

In the earlier chapter on atomic orbits we looked at how the structure of atoms and molecules might be explained in terms of electron orbital motion and without the complexities of wave-based quantum mechanics. The discussion was incomplete because it didn’t investigate whether it was actually possible for electrons to orbit in that manner. So to state the question here: using the knowledge of electrical forces described thus far, do those models describe a stable formation of atoms and molecules?

Alas not. Computer simulations based on the VDCL force functions show these models to be unstable. The electron attached to the hydrogen atom model made several orbits before being flung away. Likewise with the hydrogen molecule model. And the helium model was even less stable as it broke down after the first orbit.

Clearly something is amiss. As nice as these models appear on paper, it seems they will be unsuitable for describing a stable model of an atom or molecule, let alone a model that forces electrons to orbit at fixed altitudes and frequencies. But on closer inspection it transpired that a critical factor was overlooked in these models: the internals of nucleons.

In the preceding chapters we looked at how protons and neutrons might be constructed and there I suggested protons consist of two positive up-quarks orbiting a negative down-quark. This information was quite relevant in describing nuclear interactions. Could it also have relevance to orbiting electrons? And if so, could it account for the stability and strange ‘quantum’ behaviour we observe in atoms? The purpose of this chapter will be to investigate such questions. It won’t go into precise detail, just examine the stability of various models.

Electron-quark interactions

From a conventional physics perspective the internal makeup of protons and neutrons is considered unimportant because electrons only ‘see’ the net charge contained within a nucleus. But the ideas discussed in earlier chapters point to a different approach. Namely that we shouldn’t only consider net charge but also individual charge components because their movement affects the magnitude and direction of forces applied.

Let’s have a closer look at what this means. Below is a simplified diagram showing an electron (right) held at some distance from a proton (left).

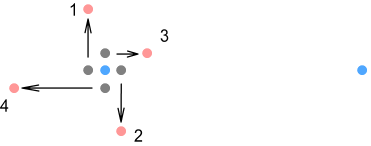
Here the up-quarks are shown orbiting in the same plane as the electron. Due to the nature of VDCL and sideways forces, as the quarks move through their orbit they exert varying degrees of force in different directions. We’ll consider four points in the orbit; located at the left, right, top and bottom positions and numbered 1,2,3,4 respectively.

First the left and right positions (numbered 1 and 2). As the position 1 quark moves up it will exert a sideways force on the electron in the downward direction. Conversely, as the position 2 quark moves down it will exert that same force but in the upward direction. As a result the two sideways forces cancel and can be ignored. Now for positions 3 and 4 (top and bottom). As position 4 moves toward the electron its force will decrease; and as position 3 moves away its force will increase. If we were to examine the net contribution from all up-quark positions (going around the circle), we would find an overall increase in the proton’s attraction on the electron.

Simply increasing a proton’s attractive force however won’t do anything other than require an orbiting electron to move faster, to adjust its centrifugal force. It won’t hold the electron in a stable orbit, nor will it force the electron to sit at fixed altitudes. But there is a more important aspect to consider.

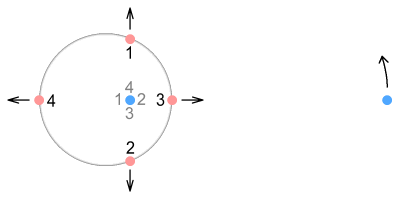
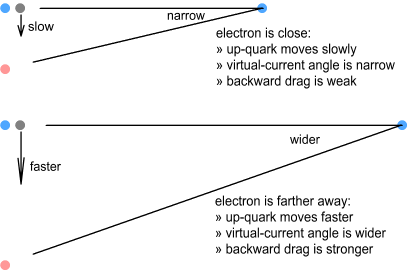
Virtual-current quarks

In the second chapter on sideways forces (part 2), we looked at something called a virtual-current particle. This is the hypothetical position of a source particle that is seen by a target, and the position we base force calculations on. For situations where the source particle is non-accelerating, i.e. moving in a straight line at constant speed, the virtual-current position can be ignored because it is the same as the actual position. In fact the virtual current position can be ignored in almost every low-velocity situation as it corresponds closely to the actual position. The proton however is neither a low-velocity nor a zero-acceleration situation. With its quarks cornering at high speed around tight circles, the proton is a situation in which virtual-current particles become important. The below diagram explains this.

Here the previous situation is repeated but this time showing both phantom and virtual-current particles. The phantom particles, shown in grey, correspond to the ones shown earlier (although closer to the nucleus here). It takes some time for the signal from an up-quark (the source) to reach the electron (the target) and in that time the quark, if it had been moving in a straight line, would have moved well outside the boundaries of the proton. For example the quarks moving up and down (positions 1 and 2) have virtual current particles far above and below, and the left and right (positions 3 and 4) have virtual particles well in front and behind the proton radius. The left-moving quark is very far out because its signal toward the electron moves less than light speed and takes longer to get there. Let’s repeat this diagram but this time using a full circle:

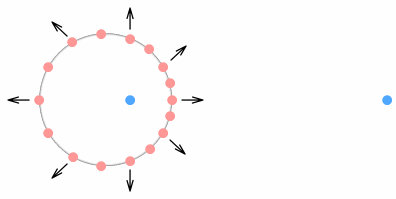
Here we see the tiny circle of the proton orbit has expanded into a large virtual-current circle (the phantoms are not shown). This is somewhat surprising because it shows that what the electron sees is not a tiny ball of closely-packed charges but a ‘cloud’ of positive charges orbiting at a large distance from a central negative charge. Although not orbiting in a normal sense because their velocity is always pointing outward. More specifically, what the electron sees is a ring of positive charges expanding away from the negative quark. Except that the ring never gets larger. To make an analogy, this ring is like a motion-blurred photograph of a speeding car – it appears to be moving forward but its position never changes.

What is the importance of this, in terms of the effect it might have on the orbiting electron? To find out we’ll again examine the four points of the quark orbit we considered earlier.

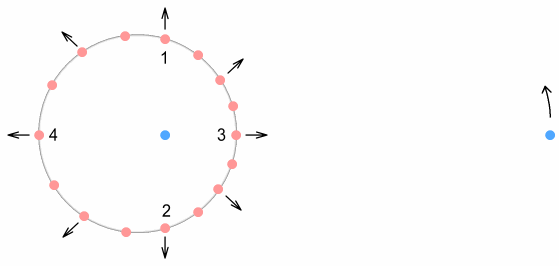
This time the electron is shown in motion around the proton. It orbits at a fixed distance, and is moving upward at this moment. Positions 3&4, corresponding to the up-quarks at the top and bottom of the down-quark, have their virtual-current positions to the left and right. Because of the direction of motion, they will cause a net increase on the force of the electron. As pointed out earlier however, this will not do anything to the electron orbit other than require it to move faster.

Quarks positions 1&2, on the other hand, are of greater interest. Especially position 2. As the electron orbits the proton, notice it is partly moving away from the position 2 quark. Therefore that quark exerts a weak backward force on the electron, slowing it down. This could be very useful because, as pointed out in the atomic orbits chapter, the sideways force from the proton will cause the electron to spiral outward. If we want to prevent the outward spiral and make an atom stable we need something to counter the sideways force. Could the backward drag from position 2 do this?

To answer this, imagine the electron is connected to the proton via a stiff rod that allows free sideways movement only (i.e. a circular orbit). The electron will be given a small push in the upward direction. Due to this motion the electron immediately experiences a promotional (sideways) force from positions 3&4 and to a lesser extent, 1&2. This causes the electron to orbit faster, resulting in ever stronger promotional forces. As the electron orbits it also feels a backward pull from position 2. Initially this force will be weak but, being directional, will grow in proportion to the cube of the velocity. At some point the backward force will equal the promotional sideways force from the other quarks (because sideways force is only proportional to velocity). The electron will then orbit at a fixed velocity.

The above scenario is interesting because it shows how an expanded ring of virtual quarks can have effects that would not be expected if the proton were treated as a point particle. But as there are no connecting rods, the electron would simply move away from the proton as it got faster. Hence the above situation is not realistic and we need to look at what happens when an electron is not constrained. See diagram.

What will happen is that the positive ring will become larger as the electron moves further away. This is because the field takes longer to reach its target, thus moving the virtual-current charges further from their source. Of course the ring does not move at all; that’s just how the electron sees it. If there were several electrons surrounding the proton, each would see a different virtual ring of differing size and position.

So as the electron moves away it sees a larger ring. Will that help slow it down? Alas not. The virtual-current particle at position 2 moves further out but its distance from the central down-quark will be in direct proportion to the distance the electron is from the centre. As a result the position 2 quark will always tug at the same angle and will not be able to increase its force on the electron and overpower the sideways force from the other quarks. This means the electron will continue to spiral out. What we need is a way for that tugging angle to increase.

Orbital speed of quarks

As we’ve seen, the size of the virtual ring depends on the distance to the electron. It also depends on the speed the up-quarks orbit the central down-quark – the faster they go, the larger the ring. As described in the chapter on nucleon structure, the speed these quarks move is determined by the size, mass and charge distribution of the quarks (both types). But could their speed also be influenced by the electron nearby? One would expect so. As the orbiting quarks moved back and forth in the electron’s field they should experience a net drag. The result of this would be to make the quarks orbit at a lower frequency when the electron is nearby and at a higher frequency when the electron is further away.

What affect will this have? Well, as the electron spirals away it exerts less drag on the orbiting quarks. As a result they will orbit faster and the angle from the position 2 quark will steadily increase. At some point the angle might be wide enough such that the backward pull on the electron is strong enough to equal the sideways promotional force. At this point the electron would stop spiralling outward and orbit at a fixed distance.

What we will have then is monatomic hydrogen – a stand-alone hydrogen atom. The electron is now orbiting at a fixed distance and is doing so at a set frequency. When viewed from the side, the electron appears as a sinusoidal oscillator. Thus it radiates this frequency into the surrounding environment and will be seen as a pure (fixed) frequency emission line on a spectrometer.

Hydrogen at different frequencies

The hydrogen atom described above emitted radiation at a fixed frequency. In reality however what we observe are a number of discrete frequencies radiating from excited hydrogen. Could the above model also account for that? In order for the electron to orbit at a number of stable frequencies we need to show that there are multiple altitudes at which both the net radial (outward) force and the net sideways force on the electron are zero.

There are many forces at work: outward centrifugal, inward electrical, sideways promotional and sideways retarding. The relationship between these is rather complicated. For example, as the quarks spin faster they increase their overall attraction on the electron, and this requires the electron to orbit at higher speed to counterbalance it. A faster electron in turn will exert less direct force on the quarks because its field takes longer to reach them. Knowing which combination of velocities and distances will result in a zero net force on the electron requires a set of equations detailing all these forces.

Finding mathematical solutions to such equations is going to be somewhat difficult. So rather than attempt a mathematical route we’ll simplify the situation by looking at two situations: when the electron is forced away from, and toward, the proton.

If the electron were to move a bit farther from the proton, the quarks would orbit slightly faster, increasing the position 2 angle and pull the electron back in. However, there is an upper limit to the quark orbit speed, and beyond a certain distance the electron would not be pulled in because the position 2 angle would not increase. At this point the electron would spiral outwards and our atom would be dismembered.

Alternately, if the electron were orbiting at a lower altitude it would move faster. This higher tangential speed would cause it to exert less force on the orbiting quarks. This in turn would enable the quarks to orbit slightly faster and hence increase the position 2 angle. Thus the orbiting electron could again feel a retarding force equal to its promotional force.

What we would have then are several altitudes at which the electron could orbit. Orbits closer to the proton nucleus would radiate higher frequencies and vice-versa. The outermost orbit (highest altitude) would emit the lowest frequency. This would correspond to the low-frequency ‘base orbit’ in Bohr’s model. The difference between this and Bohr’s model is that in Bohr’s model the base orbit is closest to the nucleus and higher frequency orbits are further out. In my model the base orbit is the outermost and higher frequencies are further in, as this diagram shows:

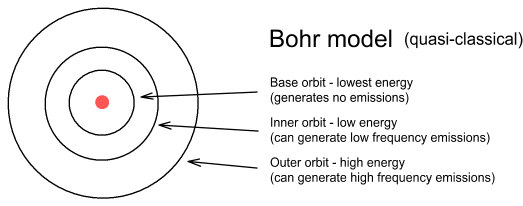
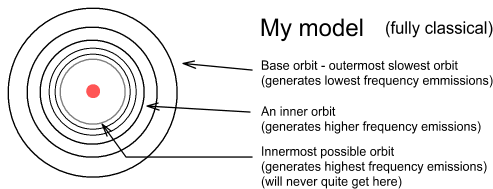
In the Bohr model there is no upper limit to the altitude electrons can orbit. In my model there is both an upper and lower limit and the distance between successive higher frequency orbits become ever smaller.

Monatomic Hydrogen Stability

The configuration described above suggests monatomic hydrogen is stable and its electron could continue orbiting like this forever. In reality however the constant radiation such an atom emits would disturb nearby atoms, causing them to emit radiation that disturbs the original atom in turn. As a result the electron orbit would eventually break down, causing its emission to cease. This is consistent with observation which tells us that emissions from radiating atoms are brief.

The Helium Atom

In the earlier atomic orbits chapter one model considered for helium was to have two electrons situated on opposite sides of the nucleus. In this way the sinusoidal radiation emitted from one orbiting electron would be 180 degrees out of phase with the other and would cancel. This model however was rejected on the grounds that (a) the net sideways force on each electron was promotional, which would cause it to spiral outward and (b) an electron might drop to a slightly lower orbit altitude, get underneath the other and eject it.

The ability described above for a hydrogen atom to hold its electron at a fixed distance however provides a clue as to how helium could also be stable. If it’s possible to hold an electron at a fixed distance from a hydrogen nucleus then why not hold two electrons either side of a helium nucleus like this:

As described in the chapter on atomic nuclei, the helium nucleus consists of two protons and (usually) two neutrons arranged end-to-end and orbiting in the same direction. So it presents the same basic charge profile as a hydrogen nucleus. Like the hydrogen nucleus, the helium quarks will orbit in the same plane as the electrons. What helium electrons will see is a set of up-quarks orbiting negative charges, and these will determine the possible electron orbit altitudes.

Hydrogen Molecules

Hydrogen’s most stable and common formation is as a molecule consisting of two hydrogen atoms bound in some manner. In the atomic orbits chapter I suggested the two atoms sit side-by-side, their electrons orbiting in the same plane and in opposite directions. In this way the electrons would cancel each other’s signal and also create a bond between the two atoms. As mentioned above however, this model failed a computer simulation test, which showed that electrons ‘despise’ running in opposite directions because the VDCL force between them becomes too great. Using the new knowledge about the rotating quarks then, can we create a stable model for hydrogen?

The helium model provides a clue. If it’s possible to make two electrons orbit on opposite sides, why not set the hydrogen atoms up like this:

Here the protons are side-by-side and the electrons orbit between them. This is like the neutron model which had the up-quarks orbiting between the negative charges. The electrons attract the protons and draw them together and the protons repel each other. This creates a stable formation.

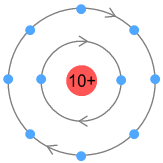
Higher order elements

Schoolbook chemistry tells us that atomic electrons are arranged in multiple shells, with each shell representing an orbit holding one or more electrons. The first of these shells holds either one or two electrons and caters for hydrogen and helium. The next shell holds up to eight and covers the second row of the period table: lithium to neon. We could draw the neon atom looking like it does in the classical sense:

Here both shells are circular paths sitting a fixed distance from the nucleus. Inside a shell the electrons are evenly spaced. To prevent VDCL repulsion both shells need to orbit in the same direction, although the inner shell electrons will move faster. The fixed orbit of the inner shell electrons will influence the electrons in the outer shell and likewise ‘quantize’ them to orbit at a fixed altitude(s). The number of electrons in a shell would need to be multiple of 2, such that a pair orbiting opposite each other would cancel each other’s signal and prevent. But why does the second shell hold 8 and not 2, 4, 6, 10 etc.? That’s difficult to answer. Perhaps there is sufficient space to hold 8 electrons and no more.

Beyond understanding how atoms behave on their own is the question of how different atoms combine to form molecules with covalent bonds etc. Unfortunately, as more electrons and quarks are added the situation becomes ever more complex and these questions will have to remain mysteries for the time being. As mentioned earlier, this chapter is intended only to describe how electrons could arrange themselves into stable formation at fixed distances from nuclei. A proper analysis will require knowing the size and charge distributions of quarks – something we don’t know as yet.