Nuclear Forces – part 2

In the previous chapter I discussed how nucleons (protons and neutrons) could be held together using only the conventional electrostatic force, and without the need for a Strong Nuclear Force (SNF). I also showed a model of how two protons could cling at close range. Well it turns out that this model is wrong. A computer simulation shows that the proton on the left will straighten itself out, resulting in the other proton detaching itself and the two protons flying apart.

The fact that this model fails is actually reassuring because we know that in reality two isolated protons won’t stick together. No helium nucleus is ever observed to consist of only two protons. Instead it always has some neutrons (usually two) with it. Likewise with other atoms: every nucleus with a given number of protons is packed with a similar number of neutrons. So if a proton can’t stick to another proton, could it stick to a neutron?

The structure of a neutron

To answer this question we need to speculate what a neutron looks like. Nuclear decay experiments tell us that when a neutron decays it emits an electron and then turns into a proton. So it seems logical to suggest that a neutron is just a proton and an electron joined together. This is a side-view of what it might look like:

The proton on the right is bent towards the electron on the left. The two up quarks can then collectively orbit both the electron and down quark. It can be shown that when these four particles are arranged as two equal-sided triangles, the repulsive force between the negative particles is exactly matched by the attractive force from the positive up quarks. The up quarks then experience an inward force that can be counteracted by the centrifugal force of their orbital motion.

So what we have is a model of a neutron that holds itself in a stable formation without the need for ‘color’ forces. The electron is much lighter than the down quark but since it doesn’t move its mass is unimportant. This disproportionate mass between the negative particles indicates why the up quarks must do the orbiting and not vice-versa.

Structure of a deuteron

Now that we’ve seen what a neutron might look like we may now consider if it could attach itself to a proton. The answer appears to be yes! Now that the electron has pinned-back the up quarks, this allows a proton to attach itself to either end of the neutron. The resulting combination looks like this:

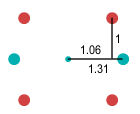
When the particles are arranged according to the above measurements and the up quarks set in orbital motion, all forces are balanced and a stable formation is found. This proton-neutron pair is called a deuteron because it is essentially the nucleus of a deuterium (heavy hydrogen) atom. The above diagram is misleading because it is a 2D representation. To be stable in a 3D environment the two pairs of up quarks need to be set at right angles and the above measurements are for this situation. Here is a 3D representation:

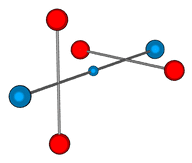
Here the electron is shown in the centre position. It could also be at either of the outer positions, but placing it in the centre makes the deuteron symmetrical and this may help if it needs to be balanced for some reason. Having the electron in the centre is important because it means that when a deuteron breaks apart it forms a proton and neutron, and not some other strange particles. So perhaps this symmetry helps the nucleons to join in this manner.

Diprotons and Dineutrons

Another thing apparent from this neutron model is that it will be somewhat difficult to join two neutrons together due to their negative charges jutting out at either side. A particle consisting of two neutrons is called a dineutron (or di-neutron) and is not known to occur in nature.

Similarly a particle consisting of two protons is called a diproton and, as mentioned above, is not found in nature either. Both facts are consistent with the proton and neutron models shown.

Various literature on this subject states that diprotons could exist if the nuclear force could be made only 2% stronger. Given that the (attractive) nuclear force is said to be 137 times stronger than the (repulsive) coulomb force however, it’s hard to see why a further 2% would be required.

But even if so, what about dineutrons? Neutrons have no charge and hence no coulomb repulsion. So we should expect their nuclear attraction to be stronger than ever. In fact we should see neutrons accumulating into huge clumps (and we don’t). The stated reason for neutron’s inability to cling is incompatible ‘spin’. But this is hardly an explanation since we don’t know what spin is. There’s a lesson here: whenever you can’t explain something, just say it’s due to spin and nobody can refute it. It seems the mainstream scientists are simply clutching at straws and won’t admit they haven’t a clue.

Fractional charges of quarks

In the nuclear particle models presented thus far, the charge of the quarks has been given as plus or minus that of an electron. Those familiar with the Standard Model of particle physics might object to point out that quarks are not charged like this.

In the early 1960’s when a physicist by the name of Murray Gell-Mann put forward the hypothesis for the existence of quarks, he speculated that the charge of an up quark was two thirds of a proton’s, and the down quark was one third of an electron’s charge. In this way a proton consisting of two ups and one down quark would have a charge of +2/3 +2/3 -1/3 = +1. The benefit of such fractional charges is that a neutron could then be said to consist of two downs and one up quark, giving it a net charge of -1/3 -1/3 +2/3 = 0; i.e. a neutral charge.

I would suggest that this neutron model must surely be wrong. We know that a neutron decays into a proton and electron. For this model to be correct, it would require that a down quark transform itself into an up quark – changing both its charge type and strength from -1/3 to +2/3 – and that an electron essentially be produced from nowhere! Perhaps this is possible but a simple ‘neutron = proton + electron’ model seems far more likely.

Putting aside the odd neutron model, does a fractional charge of quarks invalidate the particle models suggested here? It doesn’t. As will be shown, the models presented are still valid. In the proton, the force on the orbiting up quarks will be weaker but still inward. So the up quarks will still orbit the down, albeit more slowly.

In the neutron and deuteron model the positioning of the orbiting up quarks will be skewed toward the electron. Below is how a neutron and a deuteron would look if fractional charges were used:

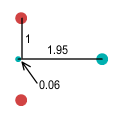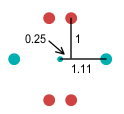Neutron	Deuteron

Observe the neutron. The -1 charge of the electron dominates the -1/3 charged down-quark and pushes it far to the right. This gives the neutron a very unstable appearance – as though the down-quark could easily be knocked away by a wayward particle or photon. Now it is known that isolated neutrons are unstable with a half life of 10.3 minutes. Perhaps this instability could be explained by fractional charges. But a problem with this is that a neutron decays by ejecting an electron, rather than a down-quark. If it ejected the quark, the neutron would become a particle with charge -1/3.

Now observe the deuteron. We know that neutrons become stable once combined into a nucleus such as a deuteron. This deuteron appears far more stable than the isolated neutron. In fact, it appears even more stable than the deuteron made of whole-charged quarks. The up quarks look to be close together, but remember they are actually at right angles so the distance between them is 1.5 units.

Here the electron is shown in the middle. As discussed above, it is important for the electron to be in the centre position for symmetry and for when the deuteron breaks apart. But what if the electron were on an outside position? Well as it happens, it’s not possible to place it on the outside because the inward forces on the up quarks would be different, requiring that the quarks orbit at different speeds. This would cause the up quarks to greatly interfere with each other. But perhaps the up quarks could orbit at different altitudes? Not so. Extensive analysis indicates that there does not appear to be any stable formation for the electron to be in an outside position.

In essence then the fractional quark charge idea fits well with deuterons but not with neutrons. Another issue is that we don’t observe these fractional charges in isolation. I will discuss this in a later chapter.

What about neutrinos?

In the above discussions of neutron decay, only a proton and electron were mentioned as by-products. So what about the neutrino – isn’t that also a by-product?

The neutrino particle was first hypothesised by Wolfgang Pauli to make up the energy difference in spin momentum. It is difficult to know whether such charge-less, mass-less particles exist but they have apparently been since discovered. Does the existence of a neutrino alter our neutron model? Observe that the neutron contains a cavity surrounded by its orbiting and still particles. Since the neutrino has no charge, it could seemingly fit comfortably inside this cavity without disturbing the neutron motion. While the neutron model presented here does not require the presence of a neutrino, this model doesn’t exclude it. It is also possible that neutrinos may be necessary for the formation of neutrons, i.e. that a neutron needs to form around a neutrino in much the same way that a rain-drop requires a dust particle to form around.

Of course this is rather speculative. A simpler explanation would be that neutrinos don’t exist and the experiments that detect them are actually measuring some other particle. I’ll discuss this further in the next chapter.

Conclusions

Neutrons can be formed by a combination of a proton and an electron that can lock into a stable formation without the need of color forces. Once formed, the neutron can then attach itself to a proton using only conventional electrostatic forces. The model here predicts that a proton cannot be attached to another proton. The Strong Nuclear Force model would predict that they can, and this is inconsistent with observation.