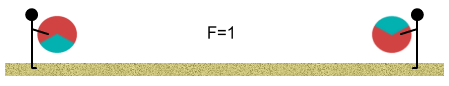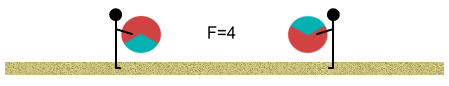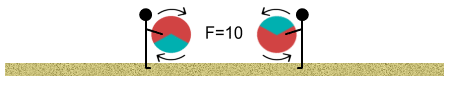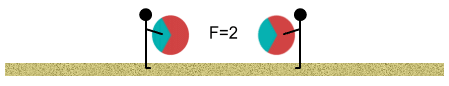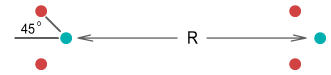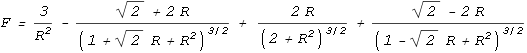Nuclear Forces
Coulomb’s law for electric charges holds that opposite-charges attract and
like-charges repel. The use of this law helps us understand how charged particles interact
at a distance. While this law may be good for explaining electrical phenomena, it does not
however explain how protons within a nucleus could stick together. After all, protons are
positively charged and should repel one another. And at close proximity such as within a
nucleus, the force between protons should be enormous and cause them to rapidly separate.
In 1935 a scientist by the name of Hideki Yukawa hypothesised that there exists a force
that could bind nucleons (protons and neutrons) together. He called this the ‘strong
nuclear force’ because it had to be stronger than the electrical force that would
otherwise push protons apart.
The strong nuclear force (SNF) was a curious contrivance that required some unusual
properties:
1. The force, while stronger than the electrical force, needed to operate only within a
short range. Otherwise it would attract protons at any distance.
2. The force needed to become neutral at even shorter distances. Otherwise protons would
be forced together, possibly extinguishing themselves as an electron and positron are said
to do.
3. The force also needed to work on neutrons which have neutral electric charge. Thus the
possibility exists that the force should probably affect all subatomic particles and also
cause electrons to cling together.
To overcome the first problem it was proposed that the SNF’s strength might vary with
the inverse cube of the distance, i.e. 1/r3. To overcome the
second it was proposed that a repulsive SNF also exists. This would need to be even
stronger than the first and work at an even shorter range, for example as the inverse
forth power of the distance, i.e. 1/r4.
With such an unusual range of forces, the SNF was shaping up to be somewhat bizarre.
Normally in three-dimensional space we would expect a force function to vary with the
inverse square of distance. Yet here were cubed and forth powers. What have we now: 4D and
5D space? [1]
Modern nuclear theory, known as the Standard Model, holds that the SNF is bought about by
the presence of special subatomic particles called ‘pions’. Pions somehow
provide exchange forces that pull nucleons together. As to how they do this is unclear.
The Standard Model also proposes a ‘color force’ that apparently holds a proton
together internally using subatomic particles called ‘gluons’. Gluons somehow
provide an exchange force that ‘glues’ a proton together. Yes, it’s
complicated!
A simpler explanation for nuclear forces
There is a much simpler explanation that fully explains how protons can
cling together without requiring the invention of peculiar short-range forces or
additional particles. This explanation fits neatly within classical mechanics and does not
violate Coulomb’s law; in fact, it’s based on it.
First let’s look more closely at a proton. As everyone knows, a proton is positively
charged. So it’s not possible for two protons to attract each other, right? Well
that’s not quite true. Yes a proton is positively charged, but that’s only its
net charge.
High-energy particle beam experiments tell us that protons are made up of subatomic
particles called ‘quarks’. Each proton consists of one ‘down’ quark
and two ‘up’ quarks. The down-quark has a negative charge, identical to the
charge of an electron. The up-quarks each have a positive charge, identical to the charge
of a positron (a positively charged electron) [2]. In other words a
proton is two-thirds positive and one third negative. This makes it overall positive with
the equal but opposite charge of an electron.
A day at the beach
To better explain this, let’s imagine that we are at the beach. We
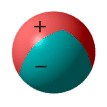
have each been handed an inflatable beach ball by an eccentric scientist. This scientist
has given each of these balls a static charge but has applied the charge in an unusual
manner. Each ball has been identically charged such that two thirds of its surface has a
positive charge and one third has a negative charge. See diagram below.
Initially we stand far apart. The balls have a net (one-third) positive
charge and this causes them push apart from each other. At this distance the force is one
unit:
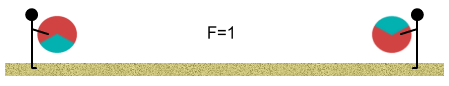
Next we start walking toward each other. As we move closer together we
each feel the balls push stronger against our bodies according to the inverse square law.
When we are at half our initial distance the force is four times stronger.
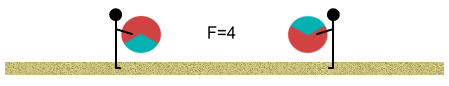
We continue walking and the closer we get, the stronger the push-back of
the balls. Then as we close in and the repulsive force appears insurmountable, something
strange begins to happen. Remember the one-third negatively charged area? Well the balls
begin to rotate in our hands so that the negative area of one faces the positive area of
another (assume that the balls can rotate in our hands without slipping out of them).
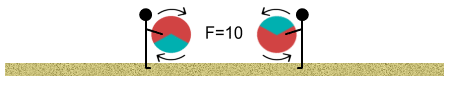
At this point the oppositely-charged areas are now closer to each other
than the like-charged areas. The inverse square law tells us that the attractive force
from the opposite-charged regions begins to have more ‘worth’ than the repulsive
force of the like-charged regions.
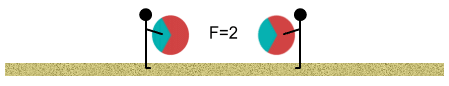
The balls may still repel one another but the repulsion is weakened. We
continue walking closer. The attractive forces become much greater, and at some point,
equal to the repulsive force; at which point there is zero net force between the balls. We
continue closer. The attractive force now exceeds the repulsive force. At this point the
two balls pull themselves together and make contact.
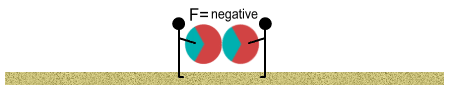
Proton beach balls
This beach ball scenario is an analogous to the forces between protons.
Each proton has two-thirds of its ‘surface’ positive and one third negative. At
a distance they repel because they are net positive; and they will repel regardless of
orientation. But if you could somehow bring them close enough together they might
reorientate such that the attraction between their opposite charges exceeds the repulsion
between their like-charges. At this point the protons would become net attractive and
‘stick’ to each other.
To see how this works we must first speculate what a proton looks like. Since the proton
is said to be composed of two positive (up) quarks and a negative (down) one, I’ll
speculate that the up quarks orbit the down quark; much like how two moons might orbit a
planet. This provides them with a stable formation; and does so without the presence of
any mysterious gluons or color forces. I’ll also say that the quarks orbit at a fixed
distance due to a quantum-mechanical restriction. Below are front and side-view diagrams:
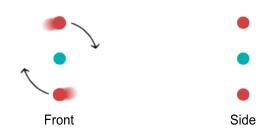
Notice the side view. Normally the up quarks will try to sit on opposite
sides of an orbit plane because they repel each other. But let’s imagine that we had
two protons and were able to bend their orbit planes at a 45 degree angle. They would look
like this:
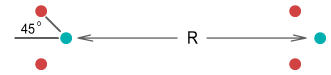
Let the distance between the protons be R. Assuming the
protons remain bent at 45 degrees, what would be the force between them as R
decreased? Calculating this requires determining the horizontal force from each quark on
one proton to every quark on the other (see function below). This is the result:
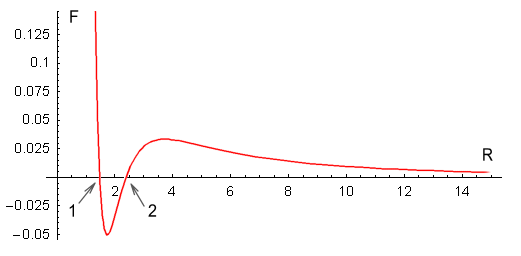
| In the above chart the distance between an up and down quark is
fixed at one unit, and the force between two such charges has a value of one unit. The
calculation of the net force is rather complicated so I’ll only show the resulting
equation: 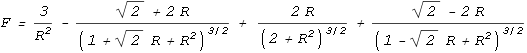
|
As can be seen, the force is repulsive at large distances, following the expected inverse
squared law. Then at closer range the force decreases toward zero and then becomes
attractive. It then eases back to zero and then becomes strongly repulsive.
The above chart suits Yukawa’s requirements to a tee. It contains all the force
elements required to hold two protons together without needing any force other than the
static electric force provided by Coulomb’s law, or any additional particles.
The protons should come to rest at point 1 on the chart. At this point
the net force is zero and any movement away from this point will force the protons back to
it. What about point 2, where the force is also zero? In theory the
protons could also stop here but the slightest movement would force the protons either
toward point 1 or fully away from each other. Stopping at point 2
would be like trying to balance a billiard ball on top of another billiard ball; it
can’t be done in practice.
When at equilibrium point, the force situation looks like this:
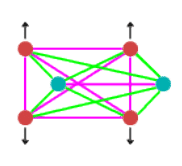
In the above diagram, purple lines represent repulsive forces, green lines
are the attractive forces and the black arrows show centrifugal force. As you can see
there are a multitude of forces involved in producing the equilibrium situation.
Now to be accurate, the above example is not fully correct because I have fixed the angles
of the orbit planes at 45 degrees without considering to what extent the force between two
quarks on the same proton would push the angles apart. I will go into more detail on the
required angles and distances in the next chapter.
Conclusion
Modern nuclear theory holds that nucleons (protons and neutrons) are held
together within an atom’s nucleus by the presence of additional particles. These
particles provide both attractive and repulsive short-range forces that overcome the
long-range repulsive electrical force and hold nucleons together at close range. However
it is possible to explain the nature of these short range forces using only the
conventional inverse-squared electrical force described by Coulomb’s law.
The Strong Nuclear Force concept requires believing that forces exist in three-dimensional
space whose strengths don’t follow an inverse square law. While this might be
possible, the SNF is an excessively complex idea that in all likelihood is untrue. The
alternative theory suggested above is far simpler and fits consistently with established
classical mechanics and electric force laws. It therefore more likely represents the true
situation.
[1] To be precise, the SNF is based on the ‘Yukawa Potential’
which contains an exponential term. No number of spatial dimensions could account for a
force function of this nature.
[2] The Standard Model suggests that quarks are not charged like
electrons and positrons, but instead have fractional values of charge. I will discuss this
in the next chapter. |