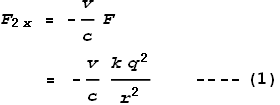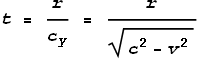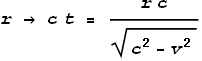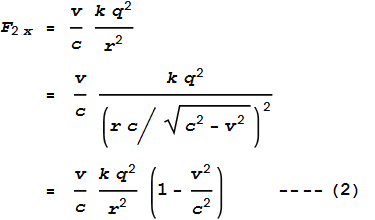The Sideways Force – part 2

We are not done yet. There is another aspect to sideways forces that needs consideration; and one that will force a revision of some earlier ideas.

The Hit Man Returns

In an earlier chapter on the Lorentz Transform we looked at a derivation of that function involving the problem of a hitman taking down a target in a drive-by shooting. Let’s now consider a variation on that. In this new situation it will be necessary for the hitman to shoot the target several times. This time road is not busy but, for some unexplained reason, the car is still not able to stop directly in front of the target. So the driver needs to drive forward-and-reverse in front of the property several times while the hitman does his job.

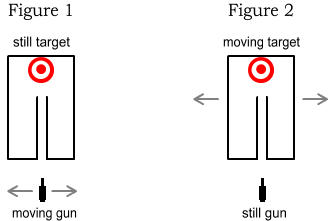
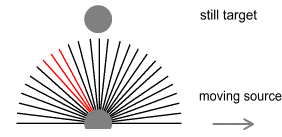
In this situation the target again stands still while the hitman moves. What would happen if the situation were reversed? See below.

In Figure 1 (left) we see the target motionless and the hitman moving. For simplicity the target is shown inside a box and at the end of a narrow tube. The walls of this tube will absorb, rather than deflect, bullets. As before the hitman can hit the target by aiming his gun at an angle to compensate for his left/right movement. So long as the car is moving slower than the bullet, there will be no problem in selecting an appropriate angle.

Now in Figure 2 (right) we see the opposite: namely, the hitman is standing still and the target is moving left and right. But since velocity is purely relative, it really makes no difference who is still and who is moving, and the hitman should have no problem in hitting the target as before. Right?

Ummm… not quite. The hitman can only shoot when the tube’s opening is directly opposite. If he aims at the moving target, the bullet will be absorbed by the inside wall of the moving tube. If he angles his gun to compensate for the target’s movement he’ll also miss because the target is only moving over a short range and the calculated angle will point at a location outside that range. Again, he will hit the tube.

Which electron is moving?

The above scenario seems odd as it appears to contradict the notion that velocity is relative. There is an analogous situation involved with charged particles. See below.

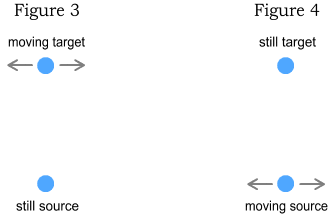
Two electrons are positioned above and below each other, a large distance apart. In Figure 3 (left) the bottom electron stands still while the top electron zigzags left and right. In Figure 4 (right), the situation is opposite: the top one stands still while the bottom one zigzags. We wish to know the force experienced by the top electron in each case.

In Figure 3, as the top electron moves left and right it experiences a sideways force because the field from the bottom electron moves through it at an angle. This force will be approximately proportional to velocity.

For Figure 4, as the bottom electron moves left and right it leaves behind an image of itself called a phantom particle (see previous chapter). Seeing that the bottom electron only moves over a small range, its phantom image can only be found within that range. Since the phantom is what the top electron sees, this means that the force direction will always be close to vertical and it will have almost no sideways component.

Radio transmission

The above situation creates a dilemma because it conflicts with our experience of radio transmission. When electrons move up & down a transmission antenna, they cause a similar movement of electrons in a distant receiving antenna. This indicates the electrons in the receiver are experiencing some sort of sideways force caused by those in the transmitter.

If this situation was equivalent to Figure 3, there would be no problem in explaining it. But it’s equivalent to Figure 4, where there is almost no force available to move the target particle sideways. According to the description of sideways force in the previous chapter, radio transmission couldn’t work. Yet we know that radio transmission does works over long distances, even with short antennas. In fact electromagnetic signals, including visible light and x-rays, can reach us from galaxies billions of light years away.

The fact that radio transmission works over long distances tells us we are overlooking some critical aspect of sideways forces: somehow the transverse (sideways) component of velocity is preserved in the transmitted electric field. How could that be?

The angled bullet

Let’s return to the original hitman scenario from the earlier chapter. The hitman angled his gun to exactly negate the forward car-movement. Consequently the bullet moved at a 90 degree angle to the car and hit the target head-on. According to our sideways force law, force must be in the same direction and thus the bullet could not exert any sideways force.

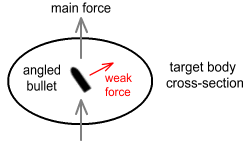
Or could it? A close-up examination of the target area (the victim!) tells a different story.

Above we see a cross-section of the bullet moving through the victim’s body. The bullet is moving vertically (relative to this page) but is doing so on an angle. As the bullet moves forward we would expect that its orientation would push the body not only forward but to the right. What we have in effect is a form of sideways force in the direction of the car.

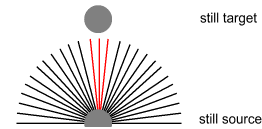
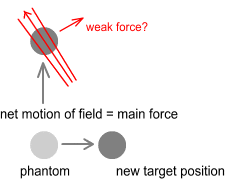
The bullet’s angle corresponds to that of the gun when it fired, which in turn corresponds to the car’s horizontal component of velocity. This means that information about the horizontal component of velocity is preserved as the bullet moves forward.

Could an equivalent phenomenon be happening with electric fields? I’m not suggesting that fields are made of cigar-shaped projectiles. But we could imagine something similar, such as lines that extend outward from the source. See below.

Above we see field lines extending from a source particle (bottom) toward a target particle (top). Both particles are stationary. The lines extend from the source in all directions but, since neither particle is moving, only the lines moving directly upward (marked in red) hit the target.

Next we’ll consider a variation on the above where the target is still (as before) and the source is moving to the right.

Here the lines that ultimately hit the target are those that emerge at an angle (shown above in red). Just like the hitman’s bullet, the backward horizontal component of field velocity must match the forward velocity of the source particle. These field lines will then move directly upward and strike the target as shown below.

Just like the bullet then, it might be supposed that the edge of these field lines causes a force toward the right and slightly upward. This would explain how electrons in a receiving antenna are able to imitate the movement of those in a transmitter – even at great distances.

Type-1 and Type-2

What we are describing here is a new kind of sideways force, and one distinctly different from the force described in the previous chapter. For the sake of distinction I’ll call this new force a ‘type-2 sideways force’, and the other one (from the previous chapter) a ‘type-1 sideways force’.

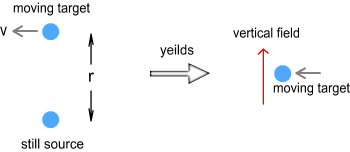
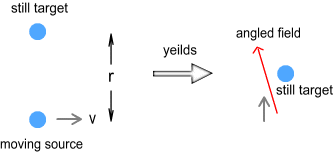
Calculation for simple situations

Let’s now derive some equations that describe the amount of type-2 sideways force in simple situations. We’ll start with two negative charges, directly above and below each other, as shown below.

They both have a charge of q, are separated by a distance of r, the bottom charge is still and the top one is moving to the left with velocity v. Here the target moves into a vertical field line (see right). As a result it experiences a backward force to the right.

How strong should this force be in relation to velocity? To make things simple, we’ll speculate that the force is directly proportional to velocity and the standard coulombs force, i.e.:

$F_{2x} = -\frac{v}{c}F\text{ }=-\frac{v}{c} \frac{k q^2}{r^2}\text{ ----}(1)$

Where F_2x is the type-2 sideways force in the x direction. The velocity is expressed as a fraction of light speed and the minus sign shows the force direction is opposite to velocity, so in this case the force is to the right.

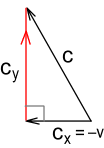
Next we’ll reverse the situation and have the top charge still and the bottom one moving to the right with velocity v. From a relative velocity viewpoint this appears to be the same situation. Yet it isn’t. In the first situation the target particle hit the field lines head on, i.e. at right angles. In the second the target was hit from behind by field lines on a slight angle as shown below.

This field line is moving directly upward but its angle gives it an effective horizontal velocity which is equal to the source velocity (v). The upward velocity is less than light speed which means that it takes longer to reach the target and hence will be weaker. Refer to the segment on phantom particles (in point 2). If we know the time taken we can determine the field strength by replacing distance r with c t. To determine the time we need to know the upward velocity. See below.

In the above diagram, the field line that hits the target must travel backward from the source particle with a horizontal velocity of -v. Using pythagoras we determine the upward component c_y to be:

$c_y = \sqrt{c^2-v^2}$

The time taken t can be determined by dividing distance r by this velocity:

$t = \frac{r}{c_y} = \frac{r}{\sqrt{c^2-v^2}}$

Thus replacing r with c t yields:

$r \to c t = \frac{r c}{\sqrt{c^2-v^2}}$

Following from equation (1) the sideways force becomes:

$F_{2x} = \frac{v}{c} \frac{k q^2}{r^2}\text{ }=\frac{v}{c} \frac{k q^2}{\left(r c\left/\sqrt{c^2-v^2}\right.\right)^2}\text{ }=\frac{v}{c} \frac{k q^2}{r^2}\left(1-\frac{v^2}{c^2}\right)\text{ ----}(2)$

As can be seen, this is very similar to (1), just slightly weaker.
( Note: F_2x is now positive because v has changed direction. )

Sideways force for opposite charges

What about the type-2 sideways force for opposite charges? Since we are speculating, the simplest approach is to suggest that the force direction will be reversed. This will give a promotional force; much like the type-1 sideways force does with opposite charges. Thus we remove the negative sign in front of the equation. This will automatically happen once we replace the q² with the standard q₁ times q₂: the force becomes promotional when q₁ and q₂ have opposite signs.

Generic equation for the sideways force

Now to determine an equation that defines the type-2 sideways force in a more general situation. To do this we’ll make use of the situation with two charged particles in the previous chapter.

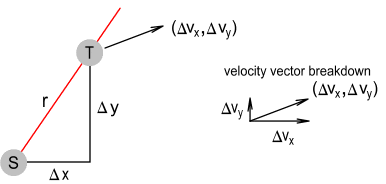
To simplify, the derivation here is based from the perspective of the source not moving, which means its position is also the phantom position and we only need refer to differences in velocity and position. Our first task will be to determine the sideways direction of velocity relative to an imaginary straight line connecting the two particles. See below.

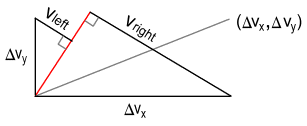
By using proportional triangles we can determine the left and right components of velocity to be:

$v_{\text{left}}\text{ }= \frac{\text{$\Delta $x}}{r}\text{$\Delta $v}_y$

$v_{\text{right}} = \frac{\text{$\Delta $y}}{r}\text{$\Delta $v}_x$

The net component of sideways velocity to the right of this line will be:

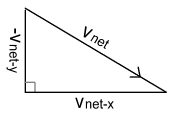
$v_{\text{net} = }v_{\text{right}}-v_{\text{left}}\text{ }=\frac{\text{$\Delta $y}}{r}\text{$\Delta $v}_x-\frac{\text{$\Delta $x}}{r}\text{$\Delta $v}_y$

We now need to extract the x and y components of this net velocity according to the below diagram.

Again we can use proportional triangles to determine to determine these components. In this case the triangle has a different orientation so the reverse distance ratios are used:

$v_{\text{net}-x} = \frac{\text{$\Delta $y}}{r}v_{\text{net} = }\frac{\text{$\Delta $y}}{r}\left(\frac{\text{$\Delta $y}}{r}\text{$\Delta $v}_x-\frac{\text{$\Delta $x}}{r}\text{$\Delta $v}_y\right)\text{ ----}(3)$

$v_{\text{net}-y} = -\frac{\text{$\Delta $x}}{r}v_{\text{net} = }-\frac{\text{$\Delta $x}}{r}\left(\frac{\text{$\Delta $y}}{r}\text{$\Delta $v}_x-\frac{\text{$\Delta $x}}{r}\text{$\Delta $v}_y\right)\text{ ----}(4)$

[See a three-dimensional form of (3) and (4) here.]

v_net-y has a negative sign because it is pointing downward. From this we can determine the net force in each direction:

$F_x = -\frac{v_{\text{net}-x}}{c}F\text{ ----}(5)$

$F_y = -\frac{v_{\text{net}-y}}{c}F\text{ ----}(6)$

Where F is the standard Coulomb force, namely:

$F = \frac{k q_1 q_2}{r^2}$

Notes:

We don’t treat push and pull fields separately. The sign on the charges determines the direction of force, hence there are no absolute operators (‘|’) around q₁ and q₂.
The force is directly proportional to velocity; there is no cubing involved. Thus the net type-2 sideways force for a source particle moving around a path and returning to its original position will be zero.
As a result of point 2, the net contribution of type-2 sideways force to magnetism will also be zero. To contribute to magnetism the force function would need to be somehow non-proportional to velocity, e.g. squared or cubed.
The above equations assume the source particle to be still or that both source and target are moving with constant velocity. For other situations it is necessary to first determine the phantom position of the source and use that instead. It may also be necessary to adjust the above ‘standard Coulomb force’ by replacing r with r = c t, as described previously.

Rethinking the Type-1 force

Based on the discussion so far, what we now have are two sets of forces that can push charged particles sideways relative to a source particle’s position. Both type-1 and type-2 work in the same direction, hence they don’t conflict. And yet it seems redundant to have both types. Not that redundancy means they can’t both exist, but there is certain situation in which the type-1 force defies credibility.

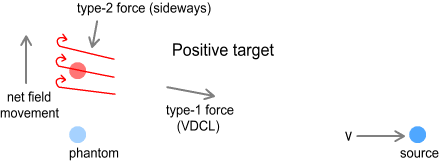
Above we see two particles: a target particle above and an electron below. The electron is moving to the right at 99% the speed of light. Its phantom image is directly below the target and, due to the great speed, its current position is far to the right. We wish to calculate the type-1 force on the target in two situations: when the target is negative and when it is positive.

Begin with the target being negative. The first step is to calculate the upward field velocity. We know that the horizontal-backward component of field velocity must be equal to 0.99c. Using pythagoras, we determine the upward velocity to be Square-root[c²-(0.99c)²] = 0.14c. Ignoring distance, charge and ‘time decay’ values, the cube of this number gives a force strength of 0.0028. This is a good result because we expect the force to be very weak in this situation.

Now for the target being positive. We already know the upward field velocity is 0.14c. Therefore to calculate the relative field strength we subtract 2c from this value and cube it, i.e. F = ((0.14c-2c)/c)³ = -6.42.

Compared to the negative case, the force on the positive target appears ridiculously large, especially considering that the incoming field was so weak. The problem is the -2c factor inside the cubing function. The idea behind the -2c factor came from the chapter on electric fields which proposed that the ‘pull field’ works by making a U-turn at double light speed. This U-turn concept appears to give a good result in one dimensional situations where the source is moving directly toward or away from the target. But it gives questionable results when sideways motion is involved.

Rather than reject the U-turn concept then, a better idea would be to ask at what speed might this U-turn occur, or better yet, in what direction. Given that the process of radio transmission indicates that fields retain information about what direction they were originally emitted in, it seems logical to suggest that the U-turn should occur along this direction rather than the direction in which the fields are passing through the target particle.

In other words we expect this:

Here we see the field moving directly upward but angled in the direction in which it was originally emitted. The U-turn occurs along this field direction and points back toward the current position of the source particle.

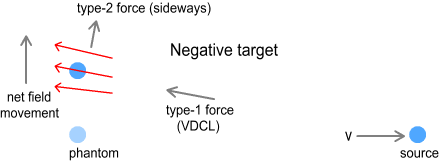
For a negative target, we should ideally be consistent with the above concept and say that the (push) force also occurs along the direction of field lines, rather than in the direction of net field movement. I.e. like this:

Here there are no U-turns and the directions for both types of forces are reversed.

We appear to have gone a full circle and come back to the original VDCL described in the chapter on relativistic mass. Gone is the original (type-1) sideways force. Instead we have a different (type-2) force to replace it. This new sideways force is similar in nature and has the similar benefit of explaining superconductivity. But it is more useful because it also explains radio transmission and is more logical for pull field U-turns.

For sake of clarity we’ll stop referring to the type-1 force as a sideways force and just call it ‘the VDCL’, and the type-2 force as just the ‘sideways force’. The VDCL no longer points to the phantom, instead it points at where the phantom would be if it continued at a constant velocity. When source velocity is constant, this position will be the same as the current source’s position. Hence knowledge of the phantom’s position and velocity is still important when dealing with an accelerating source.

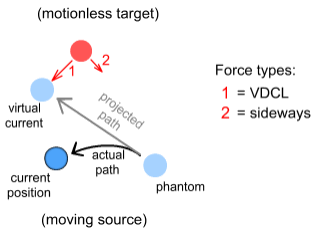
The Virtual Current particle

Given the above observations it will be very helpful to introduce a new concept: the ‘virtual-current particle’. It is defined as follows:

The virtual-current particle is the position the phantom would be in if it continued in a straight line with its at-the-time velocity up until the point at which its field hit the target.

This diagram illustrates what is meant by this:

Much like the phantom particle, the virtual-current particle represents a hypothetical position of a source particle used in determining electric forces. The virtual-current particle is useful because it can be substituted directly into the VDCL and sideways force equations. Once we know its location we no longer need to concern ourselves with phantom positions or the time-decay of fields: the equations automatically cater for it. This doesn’t mean the phantom is now unimportant because we need to know its position in order to determine the virtual-current position. The steps for determining these hypothetical particle positions go like this:

Starting with the source particle, trace its path back in time.
For each point in time, determine if the field from that position reached the target at its current (present t=0) position in time. Repeat until such historical point in time has been found.
When condition from step 2 has been satisfied, this represents the phantom position. Stop the search at this point and take note of the source position and velocity.
Assuming the phantom were to continue at that constant velocity, determine where it would be at the present time (t=0). That position is the virtual-current particle.

No doubt these instructions seem daunting, and they certainly are. Other than for simple geometric situations, these steps are best suited for a computer to crunch numerically as they can be quite involved (especially step 2).

Fortunately we can ignore these steps in most situations. For source particles moving in a straight line and constant velocity, i.e. non-accelerating particles, the virtual-current particle will be identical to the current position of the source particle. So for non-accelerating sources we can ignore both phantoms and virtual current particles and just use the source particle’s current (present) co-ordinates to calculate force. Also for particles moving at low velocity (v<<c), e.g. magnetism from electrical wires, we can ignore phantom and virtual-current particles and instead use the current source position because all particle types occupy almost the same location. These phantom and virtual-current concepts only become important in situations of high-speed and high-acceleration such as in atomic and nuclear interactions, which will be covered in later chapters.

Calculating the total force (both types together)

To calculate the net force on a charge, calculate the VDCL and the new (type-2) sideways forces separately and then add them together.

Just to restate, the VDCL will be given by this equation:

$F = \frac{k q_1 q_2}{r^2}\left.(1+\left.[q_1 q_2\right] \frac{v_t}{c}\right){}^3\text{ ----}(7)$

Where [q₁ q₂] represents the sign (+ or -) of the charges multiplied together, and v_t is the velocity of the source particle toward the target. v_t can be given by this expression:

$v_t = \frac{\text{$\Delta $x}}{r}\left(-\text{$\Delta $v}_x\right)+\frac{\text{$\Delta $y}}{r}\left(-\text{$\Delta $v}_y\right)$

We can then split this force into its x and y components:

$F_x = \frac{\text{$\Delta $x}}{r}F\text{ and }F_y = \frac{\text{$\Delta $y}}{r}F\text{ ----} (8) \text{and} (9)$

If desired we could instead redefine the field velocity as v_f = c+v_t and modify the force equation to include a -2c term for pull forces, as per the previous chapter. This would make the equation consistent with the U-turn model for pull forces. But on a practical basis, it is probably easier to express it in its above forms (7), (8) and (9). Equations (8) and (9) must then be added to (5) and (6) to calculate the net force in the x and y directions.

Conclusion

The net electric force on a charged particle can be calculated as a combination of two separate forces. The first of these will be along the direction in which the field was originally emitted from a source charge. For like charges the strength of this force will be proportional to the cube of the field velocity.

The second force will be perpendicular to the original field direction and its strength will be proportional to the sideways velocity of the field lines passing through the target particle.