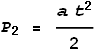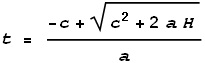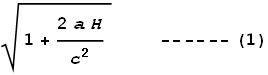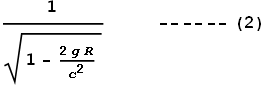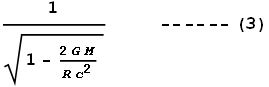General Relativity

Now that the specifics of Special Relativity have been covered, it’s time to move to the godfather of relativity theory, otherwise known as General Relativity.

General Relativity (GR) is an all-encompassing theory that fully describes the relationship between space, time and gravity. GR is often described in a complex manner, making it difficult to understand; although it need not be. It is based on three principles:

1. Everything that is true about Special Relativity (SR) for objects moving at constant velocity is also true for objects that are accelerating.

2. Gravity is indistinguishable from acceleration.

3. A free-moving body acts to reduce its degree of time dilation.

Let’s begin with the second of these since it’s the easiest to understand.

Kidnapped!

Suppose you awoke one morning and found yourself locked in a strange windowless room. Since you don’t remember being taken there you would have no idea where you were. You could be anywhere on Earth. In fact, you may not even be on Earth. For all you know you may be in outer space accelerating at a uniform 9.8 m/s² which would feel just like Earth’s gravitational field.

Suppose also that your kidnappers had kindly left behind a range of scientific equipment that allowed you to accurately measure the degree of acceleration or gravitational force. GR says that: there is no experiment you could perform that would allow you to determine whether you were experiencing gravity or a constant acceleration. In other words they are effectively the same thing. This is called The Principle of Equivalence.

For example suppose that you were in fact accelerating though space and you threw a ball horizontally. The ball would curve toward the floor just like it does on Earth. In this case the ball is actually moving in a straight line and the floor is rising to meet it. But since you’re moving with the floor it appears that the ball is curving downward.

Next suppose that you directed a horizontal laser beam across the room to the opposite wall. The beam moves in a straight line but, due to the rising floor and walls, it strikes the wall at a point slightly lower than where it started. Just like the ball, this makes the laser beam appear to curve downward (again, it isn’t really).

Now here’s the really interesting part: According to GR, since gravity is equivalent to acceleration, if you fire a horizontal laser beam on Earth it should also curve downward in the same manner. In other words light should feel the pull of gravity just as all material objects do. This is an amazing claim because we don’t think of light as being a material substance. Does it really happen? Let’s put that question aside for the moment and look more deeply into the GR principles.

Time Dilation due to Acceleration

Now to examine the first principle of GR. Again, imagine that you are in the room accelerating through space at a smooth 9.8 m/s². To make the following calculation simple, suppose the ceiling is very tall, namely 300,000 km high. Question: If someone turned on a light on the ceiling, how long would it take that light to reach the floor? Well if the room was moving at a constant velocity it would take one second because that’s how far light moves in a second. But since this room is accelerating it should take slightly less than a second because the floor is rising at an increasing pace. More importantly, the light would strike the floor at a speed slightly greater than that of light.

At this point SR steps in as if to say: ‘Tut-tut. The speed of light must always be a constant and cannot be perceived to be any faster. Therefore the observer on the floor must experience a faster sensation of time to make the light appear to move at the correct speed.’ In other words, the observer needs to experience time dilation in order to not violate SR principles.

Now let’s calculate the degree of time dilation. Consider the room in the diagram below:

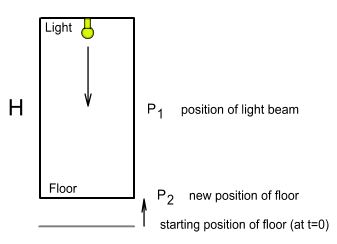
This room has a height H and is moving upward with a constant acceleration a. If a light is turned on at the ceiling it moves downward at a speed of c. How long will it take to reach the floor? Let P₁ be the position of the light beam and P₂ be that of the floor. Both measurements are the distance to where the floor would be if it continued at a constant velocity from the instant when the light was turned on (to simplify, assume the floor was initially at rest – the distances will then be to its starting position). As the light beam moves downward its position at time t will be:

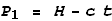
And the position of the floor will be:

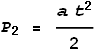
The two will meet when P₁ = P₂ at the time:

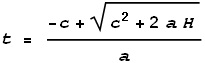
How fast will the beam be moving when it hits the floor? The floor will be moving upward at velocity a * t and the light beam downward at c. Adding these together we get:

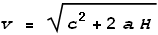
This velocity is greater than light. So to calculate the degree of time dilation needed to slow it down to c we take the ratio v/c:

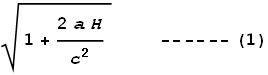
This is like the GR equivalent of the Lorentz Transform (LT) for SR. It shows how much faster time should run according to acceleration and height. For small values of acceleration this closely approximates to (using binomial expansion):

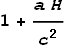
Problems with the GR time dilation formula

Now let’s look at some anomalies in the above formula:

1. When this formula was derived, the movement was in the direction of acceleration. Whereas with the LT, the movement is always assumed to be at right angles to the observer (see earlier chapter). This appears inconsistent.

2. If acceleration is negative, i.e. the floor is accelerating away from the light, time should instead slow down. With the LT, velocity direction makes no difference because the velocity term is squared. So GR time dilation should both speed up and slow down the sensation of time. The significance of this is explained below with clocks.

3. The formula says that an accelerating object (such as the floor in this example) should experience relative time dilation. But relative to what? Presumably relative to something that isn’t accelerating. The only reference object here is the ceiling light. But that ceiling light is accelerating at exactly the same rate as the floor so there shouldn’t be any time dilation between the two.

4. The formula depends both on the acceleration a and the height H. This appears odd because we should expect the dilation to be based only on acceleration. After all, the LT depends only on velocity. And what is H? It is an arbitrary height of the ceiling. If you moved the ceiling the result would be different. Or if there were several lights at different heights within the room we would calculate several different time dilations.

5. The formula assumes the room contains a vacuum. If the room was filled with air or other transparent material, acceleration should have little effect. That’s because once an atom has absorbed a photon the atom will emit a new photon with the speed of the atom added to it (see other chapter for fuller explanation). Does this mean GR time dilation won’t occur within an atmosphere?

The Triple Clock Dilemma

In the earlier discussion on SR a number of logical inconsistencies were pointed out involving moving clocks. A similar problem exists with GR. Consider the below diagram:

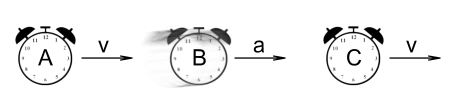
Three clocks A, B and C are initially moving to the right with an identical velocity. They are perfectly synchronized and according to SR, should remain that way since there is no relative motion.

Suddenly clock B begins to accelerate by steadily increasing its velocity. According to GR time dilation should now occur. B is accelerating away from A, so B should slow down relative to A. B is also accelerating toward C, so B should speed up relative to C. Meanwhile A and C continue have no relative motion and should remain synchronized. Mathematically that’s:

B<A and B>C and A=C.

Again we have another impossibility.

Time Dilation due to Gravity

Now that we have determined the time dilation for a constant acceleration we can do the same with gravity. Here’s how the theory goes:

Suppose there were two people: one on the Earth’s surface and the other at the Earth’s centre (assuming that’s possible!). At the centre of the Earth the net gravity is zero because the pull comes equally from all directions. Let the person at the centre be called A and the one on the surface be called B. See diagram:

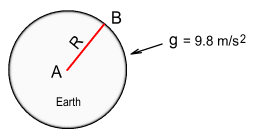
Now A fires a laser beam toward B. How long does it take the light to reach B? According to classical mechanics the time taken will depend only on the Earth’s radius. However GR has other ideas...

Since B is experiencing the downward pull of gravity, this is equivalent to experiencing a steady upward acceleration of 9.8 m/s². The Principle of Equivalence says that we can base our calculation on the assumption that the Earth’s surface is accelerating upward at this rate. What this means is that the light beam will take longer and will be moving slower when it reaches the Earth’s surface. It’s almost as if the pull of gravity were slowing the light down. In order to not violate SR then, the sensation of time at the surface must slow down to make the light appear at the correct speed.

In other words B must be in a slower time frame relative to A. Put another way, clocks in a high gravitational field must tick slower than those in low gravity, even though neither are experiencing any acceleration (putting aside the Earth’s rotation).

Calculating the Gravitational Time Dilation

Okay let’s now figure out just how much dilation should occur due to gravity. This will be easy since the calculation has already been done for a fixed acceleration – see formula (1). Simply by replacing height H with the Earth’s radius R, and acceleration a with minus g (because the direction is away from the light source), we determine the velocity of the light striking the surface will be:

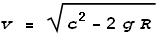
The degree of dilation required will be the ratio c/v – in this case we use the inverse of the earlier ratio in order to make its value greater than 1:

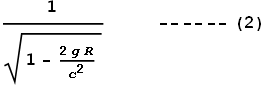
This tells us how much slower time should move at the surface of a planet of radius R and surface gravity g, compared to a point of zero gravity. For small values of gravity this closely approximates to:

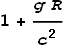
Using Newton’s gravitation equation we can also rewrite (2) as:

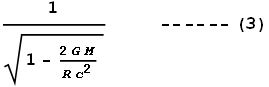
Where G is the gravitational constant and M is the mass of the Earth or some other large spherical object.

Problems with the GR time dilation (for gravity) formula

One benefit this gravitation formula (2) has over the acceleration formula (1) is that gravity will always be positive. This means that the triple clock problem won’t be an issue. Nevertheless this formula still has a problem: namely the inclusion of the radius R into the equation.

For example, suppose there was a planet that had half of Earth’s diameter but made of a material of double the density. The surface gravity on this planet would be identical to Earth’s. However due to the formula including radius into the equation, time dilation would be only half as much. This appears to violate the Principle of Equivalence which states that there should be no difference between the two because gravity is the same.

The Black Hole conundrum

A more interesting question arises with regard to high levels of gravity. Notice that the above ratio (2) has a denominator that could potentially become zero. This should theoretically happen for large values of gravity, and when it does, time dilation should become infinite. This means that time on the surface will come to a complete stop. Also notice that this term is contained within a square root which would be a problem if its contents became negative. Since it is impossible to have square roots of negative numbers (in the real world) this implies that there must be some theoretical upper limit to gravity or that something very strange must happen if gravity tries to exceed that limit.

GR proponents submit that when an object becomes this large its gravity will prevent everything from escaping, including light. Such an object is called a ‘black hole’ because no light could emit from it. Furthermore if the object becomes any larger, e.g. by adding extra mass, something must happen to prevent the term within the square root from becoming negative. One way this might happen is for the object to enlarge its radius, making that term positive – see formula (3). However there is no reason why a now even heavier object should expand; if anything the increased gravity should force it to shrink. But the moment it did shrink gravity would increase to a larger amount and make that term even more negative. Therefore it was proposed that at this point the object will suddenly collapse into a point of zero size while still maintaining its mass and take on some sort of infinite gravity. This point-object is referred to as a ‘singularity’.

To determine the dimensions of such an object (prior to its collapse) we’ll assume it to be composed of a substance known as neutron-star matter. This is what neutron stars are said to be composed of: entirely of atomic nuclei. It has a density of 2x10¹⁷ kg/m³ which is very close to the density of an atom’s nucleus [1]. Substituting this density into the appropriate equations we find that a black hole should have the following attributes:

Radius  = 28350 m
Mass     = 1.91x10³¹ kg
Gravity = 1.58x10¹² m/s²

So this black hole has a diameter of 56.7 km – about the size of a major city – and a mass 10 times heavier than our Sun. And most impressively, a surface gravity 160 billion times greater than Earth’s!

Could such things exist? Certainly there are plenty of stars with enough mass to form the above object if they were compressed into neutron-star matter. And if light is bent by gravity, even to a slight extent, it is certainly conceivable that it might be bent backward under such extreme gravity.

Well there is an easier way to reproduce this situation without resorting to enormous gravity. Namely that the GR formula (2) contains a radius term and this allows us to achieve the same infinite dilation under low gravity conditions.

For example, it can be shown that a planet made of a material with uniform density of 7.65 micrograms per cubic metre and radius of 4.59x10¹⁵ meters (about half a light year) will have a surface gravity equal to Earth’s. But due to its enormous radius the time dilation on the surface will be infinite; i.e. time will come to a stand-still and not even light could escape, even by a short distance. This is despite there being only Earth-strength gravity. Furthermore GR predicts that it will be impossible for this planet to be even one metre larger because the term inside the square root would then become negative. Does this seem correct? There appears to be no logical reason why such a planet should suddenly collapse into a singularity point.

It turns out that such speculations are unnecessary because the proper gravitational time dilation function contains a much-overlooked term that prevents singularities from occurring. This will be covered in the next chapter.

The Weak Equivalence Principle

Getting back to the Principle of Equivalence described earlier, there are actually two of these.  The first, that gravity is indistinguishable from acceleration, is known as the Equivalence of Acceleration or the Strong Equivalence Principle.  The second is the Equivalence of Mass or the Weak Equivalence Principle.

What the second says is that gravitational mass is directly proportional to inertial mass.  That is, an object experiences a gravitational force that is directly proportional to its inertia.  Put more simply, all objects will free-fall in a vacuum at precisely the same rate.

As far as we can tell this is statement is quite true and the experiments support it.  But one wonders, why say it at all?  This principle is not telling us anything we didn’t already know from Newton’s equation: F=GMm/r².  Newton, in his Principia, made no mention of ‘gravitational mass’ nor suggestion of different type of mass.  The big M and little m in that equation referred originally only to ‘mass’, and without saying what type it was.

The concept of gravitational mass it seems is being used to suggest a betterment of GR over classical mechanics.  While GR does have some improvements over the Newtonian description of gravity, as will be discussed in the following chapter, this is not one of them.  Strictly speaking, this second equivalence principle is a not a statement about GR but of classical mechanics and should not be considered part of GR theory.

Continued in part 2.



[1] http://heasarc.gsfc.nasa.gov/docs/xte/learning_center/ASM/ns.html