What’s wrong with the
Lorentz Transform?

In the previous chapter we looked at how the Lorentz Transform (LT) was derived and how it can be applied to calculate time differences. Could there be faults with this equation?

When deriving the LT, note that the light source was moving at right-angles, i.e. at 90-degrees, to the target. If you accept the Special Relativity (SR) premise that light must always appear to be moving at the same speed for any observer, then the LT is perfectly valid for this situation. But problems arise when the source velocity is not aligned with the LT derivation.

In all manner of physics texts that discuss SR, the LT appears to be readily applied to situations that don’t fit the LT assumptions. For example when a charged particle is accelerated in a vacuum tube, the force applied to the particle is in the same direction of the particle’s movement. This is a one-dimensional situation, yet the LT, which is based on a two-dimensional perpendicular force, is used to determine the SR effects on the particle.

Such blind application of a specific-situation formula to all situations may yield invalid results. Here I will attempt to derive more appropriate LTs for various situations as well as a general formula.

One dimensional situation

Let’s do another derivation for LT, but this time the light source will be moving directly away from the target. See diagram.

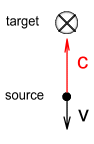
car shooting at target

The source projects a beam at the target with velocity c while moving away from the target with velocity v. Let c₂ be the velocity at which the light hits its target. Deriving the LT for this situation gives:

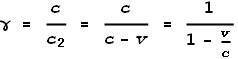
$\gamma = \frac{c}{c_2} = \frac{c}{c-v} = \frac{1}{1-\frac{v}{c}}$

It looks similar to the original LT equation but without the squaring. It also has the same requirement that the velocity must always be less than c otherwise it will not reach the target, i.e.:

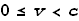
$0\leq v<c$

Now we will do the derivation again, but this time the source will be moving towards the target with velocity v. See diagram.

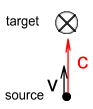
Deriving the LT gives:

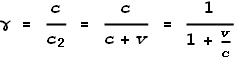
$\gamma = \frac{c}{c_2} = \frac{c}{c+v} = \frac{1}{1+\frac{v}{c}}$

As expected it’s the same equation; only the sign on v has become positive. In this case the time-sensation at the target must speed-up relative to the source in order for the light to appear the same speed. But an interesting difference to note is that there is no requirement that velocity be less than that of light, i.e.:

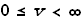
$0\leq v<\infty$

This is because, no matter how fast the velocity, the time-sensation at the target could theoretically always be fast enough to make the resulting light speed c₂ appear the same as c.

A General Lorentz Transformation Equation

Now that we’ve shown that the LT may need to vary depending on the direction of movement of the source, let’s derive an equation that should hold true for any direction of velocity. See below diagram.

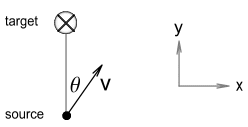
Here the source is moving at velocity v and at an angle θ away from its target. In order for the light to hit the target we need to angle the beam to compensate for the component of velocity along the x-axes. Let v_x and v_y be the velocity along the x and y axes respectively. We calculate them to be:

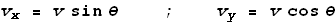
$v_x = v \sin \theta \text{ };\text{ }v_y = v \cos \theta$

Now to tilt the beam backward along the x-axes; we show the velocity components are:

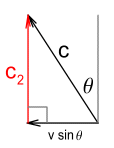
Where c₂ is the velocity that the light hits its target. Trigonometry and pythagoras reveal:

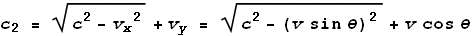
$c_2 = \sqrt{c^2-v_x{}^2}+v_y = \sqrt{c^2-(v \sin \theta )^2}+v \cos \theta$

So the LT will be:

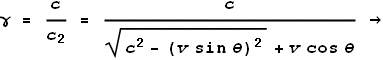
$\gamma = \frac{c}{c_2} = \frac{c}{\sqrt{c^2-(v \sin \theta )^2}+v \cos \theta } \to$

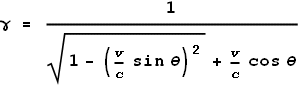
$\gamma = \frac{1}{\sqrt{1-\left(\frac{v}{c} \sin \theta \right)^2}+\frac{v}{c} \cos \theta }$

The above equation gives a general result for any source velocity v at any angle θ away from the target. Let’s look at a few special cases for different values of θ.

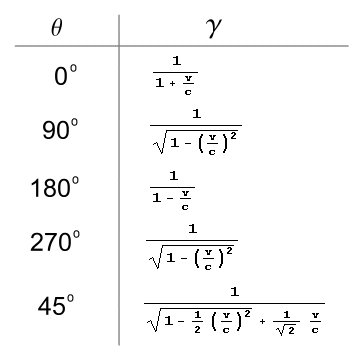
From the above table we see that when θ is 90 or 270 degrees (right-angles), we get the conventional form of the LT. When θ is 0 or 180 degrees, we get those equations given by the one-dimensional derivations above. When θ is 45 degrees, we get a more complex formula that doesn’t fit with conventional SR theory.

Limitations:

This General LT equation has some limitations. Namely, the velocity along the y-axes cannot exceed the speed of light in the opposite direction and the velocity along the x-axes cannot exceed the speed of light in either direction:

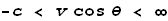
$-c < v \cos \theta < \infty$

and

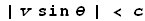
$|v \sin \theta |< c$

Conclusion

Which LT is correct? Does the conventional LT apply to all situations or should a more general form, which takes the angle of approach into account, be used for non-perpendicular motion?

It would seem that the general form of the LT given here should be more appropriate. However I have reason to believe that this may also be wrong. I will discuss in a later chapter what a more reasonable solution might be.

What’s wrong with the Lorentz Transform?

One dimensional situation

A General Lorentz Transformation Equation

Conclusion

What’s wrong with the
Lorentz Transform?