The de Sitter Effect

In the early 1900s were two competing theories about the nature of light. One held that it was ballistic and the other that it was relativistic.

The ballistic theory described light as behaving like projectiles and postulated its measured speed would vary according to the velocity of the emitting source. For example, if a source were moving toward a target, the time taken for light to arrive would decrease and an observer at the target would measure the light to be moving at c+v, where v is the source velocity. Conversely if the source were moving away, travel time would increase and the observer would measure the light to be moving at c-v.

Then there was the relativistic theory, which held that light will always appear to move at the same speed and the time taken to reach a destination will not depend on the velocity of the source. In other words, an observer will always measure the light to be moving at c, regardless of v.

Two key individuals represented opposing sides of the debate. Walter Ritz argued for the ballistic theory and Willem de Sitter argued for the relativistic one.

De Sitter suggested that if the ballistic theory was true then binary stars, i.e. a pair of stars orbiting each other, would appear different. If two such stars were in orbit and the Earth was roughly in their orbit plane then the light from these stars would take differing amounts of time to reach here.

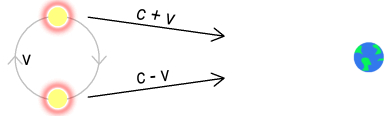
The above diagram explains this. Here two stars orbit clockwise with velocity v. The light from the top star moves toward earth at velocity c+v and the light from the bottom star at c-v. Thus the top star’s light takes slightly less time to reach earth. If the stars were nearby this would be of little importance because v is small relative to c and the stars would always appear at opposite sides of their orbit. But over a long distance this time difference becomes large. As a result the light signals may arrive out of sequence and we would observe the stars to be not opposite each other. In an extreme case we might see both stars on the same side of an orbit.

De Sitter studied a number of binary systems but in each case did not observe any such resequencing. Further studies by other astronomers have confirmed his findings. This is known as the de Sitter double star experiment.

Hypothesis confirmed?

There can be little doubt that the findings of de Sitter and others confirm that the light from both stars travelled to earth at the same speed. And this certainly appears as impressive evidence that light moves at a constant speed regardless of its emitting source. But how could that work?

If the light came from two separate sources and had to move at the same speed relative to an arbitrary distant receiver, then how would the light ‘know’ how much to adjust its velocity before it reaches that receiver? And if there were observers on either side of the star system, how could it make such adjustments to suit both observers?

Could this mean the inverse-logic of relativity theory, in which the observer determines the light’s speed, is correct after all? Or could there be a more logical explanation?

I believe there is and I’ll demonstrate with a simple analogy.

Through the looking glass

Consider the below diagram showing a laser and glass block.

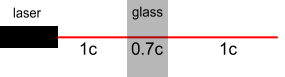
The laser beam starts at the left, passes through the glass, then exits the right of it. We know that light slows down as it passes through a transparent medium. The amount of slow-down is determined by the reciprocal of the refractive index of the medium. In the case of glass it’s around 1.52. But let’s simplify things by making it 1.43. This makes the slow-down amount 0.7, i.e. 70% of light speed.

So as the beam moves through the glass it is going at 0.7c. But what is this speed relative to? To the glass of course. Once the beam enters the glass it starts moving from atom-to-atom within the glass. Each atom becomes a new launch point for the light and that is what the beam moves relative to. To make a weak analogy, it is like someone running first on dry land then through waist-deep water: the water is the medium that determines current speed, not the dry land.

The beam then exits the block and returns to its full speed. It is now travelling at c. But relative to what – the laser or the glass? Again: the glass. The beam can no longer be influenced by the laser since it left that long ago. The final layer of atoms in the glass represents the beam’s most recent launch point so they are what determine the beam’s current speed.

We’ll now complicate the situation a little as shown:

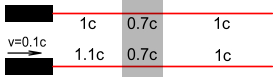
Now there are two lasers. One is standing motionless and the other is moving toward the glass. On the other side of the glass is an observer who will monitor the beams.

Assuming the ballistic theory of light is correct, the light from the moving laser will strike the glass at a slightly higher velocity. For arguments sake we’ll say the laser is going at 0.1c. So the two beams will hit the glass – one at c and the other at 1.1c.

The beams strike the glass. Then what? They both slow down of course. But by how much: does the ‘motionless’ beam slow to 0.7c and the ‘moving’ beam to 0.8c?

Answer: they both slow to 0.7c. The beam is now inside the glass and is moving relative to it. The initial speed of the laser can no longer have any effect on the current beam speed because, as before, the beam is now moving from atom to atom within the glass. Those atoms are what control the speed.

The beams then reach the other side of the glass and exit. The beams now go back to full speed: c. But relative to what – the lasers? No, the glass of course! Like the earlier example, the original beam speed is no longer important. The beams exiting the glass now move with identical speed.

This is not to say the beams will be identical in all aspects. The beam from the moving laser strikes the glass at a higher velocity and its light waves will appear to have a frequency 10% higher. This frequency will be preserved throughout the process. And the observer will see the moving laser beam as having a higher frequency – a Doppler shift!  But the final velocity of both beams will be the same: c.

Now let’s apply this analogy to our binary stars.

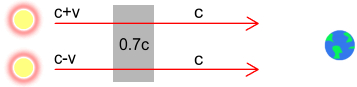
The above diagram shows the binary stars with their motion as before and Earth in their orbit plane. Now imagine we could place a sheet of glass just in front of the orbiting stars.

The light from these stars would strike the glass at varying velocities: sometimes faster than light and sometimes slower. But the instant it hit the glass it would slow down to 0.7c. It would then exit the glass and leave at speed c. Just as with the moving lasers, this exit speed would be relative only to the glass and not the rotating stars. The light from both stars would then continue all the way to Earth, each at the same speed.

Mister, got any gas?

Okay, so there are no giant sheets of glass in space. This is just an analogy. But what if there was something else? Glass is not the only refractive material. There are plenty of others. Of which we are in right now: air. So what if there were was large wall of air in front of the stars – would that have the same effect? It certainly would.

Okay there is no air-wall either. That is also an analogy. But there may be something else – gas. We know the space in our solar system is not a complete vacuum. We also know our sun throws out a lot of particles, which we call solar wind. So what if those binary stars threw out a lot of solar wind, or rather, stellar wind? And what if this caused them to be surrounded by a weak layer of gas – would that cause their light to slow down and then resume to full and identical speed upon exiting?

It stands to reason that it would. Once the light has left this surrounding gas layer it would continue toward earth at the same speed. Astronomers would observe the star rotation sequence to be the same as it would be observed close to the stars. That is, the stars would appear perfectly synchronised.

Although, their light will not be identical. As with the moving lasers, the stars will have a Doppler shift which will increase and decrease in frequency, and this frequency shift will be preserved all the way to Earth.

So there you have it, a straightforward explanation. No strange relativity requirements. Just an interstellar gas medium. I’ll have more to say on this topic in a later chapter on cosmology.