Why Time Dilation
must be Impossible
A central tenet of Special Relativity (SR) is the idea that the experience of time is a
local phenomenon. Each object at a point in space can have its own version of time which
may run faster or slower than at other objects elsewhere. Relative changes in the
experience of time are said to happen when one object moves toward or away from another
object. This is called ‘time dilation’ and can cause clocks to run at different
speeds in different locations.
Here’s how it happens: Suppose we have two clocks: A and B, which are known to be
very accurate. Clock A is standing still while clock B zooms toward it, narrowly missing.
As B passes A, we observe that they are perfectly synchronized. Clock B then continues to
move away from A as pictured below. SR tells us that because B is moving away from A, its
time will be running slower than A, and will gradually fall behind time-wise.

But wait. Is B moving away from A or is A moving away from B? Since
velocity is purely relative, there’s no way of knowing. In this case, perhaps A
should instead be running slower than B; or more properly, perhaps each should be running
slower than the other. To suggest that two clocks could both run slower than each other is
a seeming absurdity that defies all logic; even within the difficult ideas that SR asks us
to follow. It is the mathematical equivalent of saying: A>B and B>A; which is
impossible.
To complicate the situation a little, let’s say there are three clocks: A, B and C.
As before, A is standing still and B is moving to the right. C is meanwhile moving to the
left of A with the equal and opposite velocity of B. See diagram:

SR tells us that C and B must be recording time more slowly than A, and A
should slow down by the same degree relative to C and B. It also tells us that C should be
going slower than B, by a greater degree than relative to A, and likewise B should
slowdown the same amount relative to C. Mathematically this is:
A>B and B>A and C>A
and A>C and C>>B
and B>>C.
Confused?
The Time Travelling Twins
A story often told to demonstrate the implications of SR time-dilation is
that of the travelling twins; also known as the twins paradox. It goes something
like this:
A pair of identical twins, named Alpha and Beta, decide to journey to a nearby star where
a new planet has been discovered. The planet is 10 light years away from Earth and the
twins have at their disposal a space ship that is capable of travelling at near the speed
of light. However the ship is only big enough for one occupant. So it’s decided that
Alpha should stay at home while Beta make the journey alone. They estimate the round trip
should take about 20 years.
The journey begins. Once outside of Earth’s gravity, the ship accelerates at a
comfortable rate of 9.8 m/s2 (equal to Earth’s gravity), and reaches light
speed in just under a year. To fit within the SR speed limit, we’ll say that the
ship’s top speed is 99.99% of light speed. The ship then cruises at a constant
velocity for the next 10 years. As it approaches the planet, it then decelerates at the
same rate until it stops.
Beta then gets out, takes pictures, collects samples etc, and then climbs back into the
ship for the journey home. The return journey follows the same pattern of acceleration,
cruising and deceleration as before, until it reaches Earth. A chart of the ship’s
velocity would look like this:
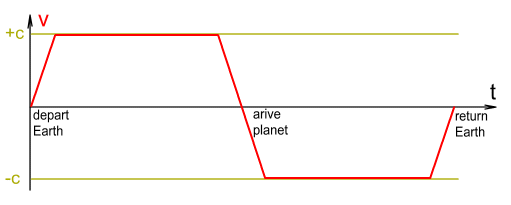
Many years later, Beta’s ship returns to Earth. It lands gently and,
as the roar of its mighty engines subside, a crowd of onlookers gather round. Twenty years
have passed and Alpha is waiting anxiously by the docking bay for the return of his
brother. As he stands waiting, we notice that he is visibly different. The sands of time
have aged him: his face, hair, and body no longer hold the youthful looks he once had when
Beta departed all those years ago
The hatch opens, and as Beta steps out, Alpha notices that his brother has barely aged,
looking much like the day when he left. In fact while everything on the Earth has moved
twenty years forward in time, Beta has aged little over a year. All of the ship’s
time keeping instruments have likewise barely moved in comparison to Earth’s clocks.
SR tells us that Beta has experienced time-dilation. The closer Beta got to the speed of
light, the slower his clocks ticked, and the slower he aged, relative to Alpha. Beta had
no awareness of this because all his bodily functions, and even his thoughts, slowed
similarly.
But hang on a minute... Was Beta moving away from Alpha or was Alpha moving away from
Beta? Both classical mechanics and SR tell us that velocity has no absolute measure and
can only be measured relative to something else. Beta looks out his rear window and sees
Alpha moving away from him at the same speed as Alpha sees Beta’s ship move away from
Earth. In other words, this:
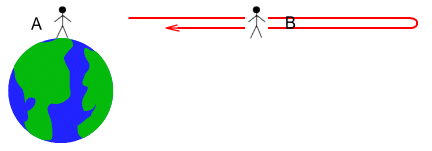
Is the same as this:
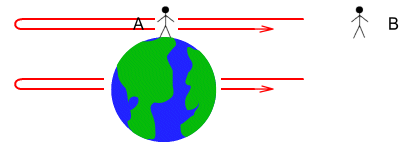
So why not have Alpha stay young and let Beta age instead? It’s the
same thing. Or let’s take it to the extreme and say that, when the ship returns, they
are both younger than each other? This is the same situation that I’ve described
above with the moving clocks, albeit with one small difference...
Effects of Acceleration
Opponents of the above argument may point out that we cannot simply
reverse the roles of Alpha and Beta because they do have a difference; namely that Beta
experienced acceleration whereas Alpha did not. That’s true. Beta experienced both
acceleration and deceleration in shifting between rest and near-light speeds. However I
would argue that this acceleration cannot account for the time differences for the
following reasons:
1. Time dilation calculations are based mainly on velocity, not acceleration. If speed was
not an issue, then it shouldn’t make much difference if the top speed was only 90%
light speed instead of 99.99%. But the Lorentz factor for 0.9c (γ=2.3) is very different from 0.9999c
(γ=71)
2. The acceleration/deceleration occurs over only brief periods of the trip – see the
above velocity chart. If acceleration was the deciding factor for time-dilation, then it
should make no difference if the destination was 20 light years away instead of 10. Better
yet we could simply remove the cruising portion of trip; i.e. immediately decelerate after
reaching top speed, and get the same result.
3. The acceleration experienced by Beta is mild; it is only Earth’s gravity strength.
If acceleration of such mild degree could allow Beta to take 20 years off his life, then I
propose we could sit in a spinning centrifuge for a few years to achieve the same. Since
the direction of the acceleration is unimportant (the net acceleration of Beta’s
journey was zero), it shouldn’t matter that the centrifuge’s acceleration is
constantly changing direction.
The reference frames argument
This leads us to the standard explanation of this anomaly, known as the
‘accelerated vs. inertial reference frames’ argument. Basically it states that
Beta shifted into a different ‘time frame’ due to his initial acceleration
– whereas Alpha did not accelerate and stayed in the same frame. This made Beta
experience time dilation rather than Alpha. An important point about the argument is that
acceleration is not what determines the degree of dilation – that is still done via
velocity. Rather, acceleration is what enables dilation to occur.
From a logical perspective this makes no sense because it says nothing about the amount of
acceleration required. Essentially it is saying that, while zero acceleration won’t
change a ‘reference frame’, a non-zero acceleration of any amount changes it
completely. For example Beta’s acceleration may be a billion-trillion times weaker
than Earth’s gravity, yet that is all that’s needed to make Beta age 71 times
slower than Alpha, rather than vice-versa. If acceleration was a determining factor in the
degree of dilation then it should be incorporated into the LT describing it. But the fact
is, it’s not.
And from a practical perspective the ‘frames argument’ fails completely. Because
Alpha, left behind on earth, cannot stand perfectly still and will be accelerating all the
time. As the earth rotates and orbits the sun he experiences acceleration. Even if both he
and the earth were somehow completely motionless, the molecules in his body will be
constantly vibrating with heat, and vibration involves acceleration. Therefore an argument
that favours non-zero accelerating bodies over zero-accelerating ones could never apply in
a real situation.
Dual changes in time
One might argue that time-dilation may yet be possible if it affected both
bodies equally. This is not a belief of SR but I’ll discuss it here.
In the example above with two clocks, if both clocks slow down by the same amount when in
motion, then each would still show the same time afterward. In other words, time dilation
may have occurred but we would have no way of knowing it. This argument holds true for two
clocks but it falls apart with three. In the example with three clocks A, B and C (above),
B ran slower than A, and slower again than C. So it is not possible for all three clocks
to run slow by an equal amount.
Directionally dependent time changes
A final consideration is the possibility that time dilation could occur if
it changed with direction. E.g. Beta could age more slowly than Alpha while travelling
away from Earth, then age more quickly during the return trip, restoring his age to match
Alpha. The net result is that time dilation would have occurred but neither twin would
know it. This is not a belief of SR either but it should be addressed for completeness.
While this possibility holds true for two observers, it falls apart for three. Suppose we
have the three observers A, B and C as pictured.
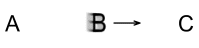
A and C are motionless with respect to each other, while B moves away from
A and toward C. If time dilation was directionally dependent then B’s clocks should
move slower than A’s, but faster than C’s (or vice-versa, if you prefer). But
this would contradict the relation between A and C whose clocks need to move at the same
speed. Mathematically that’s:
A>B and B>C
and A=C
Again, another impossibility.
Conclusion
SR proponents would have us believe that the fountain of youth awaits us
inside a high speed rocket ship, or on a lifetime of non-stop jet travel, if only we can
make them fast enough. Nice if it were true.
Based on the reasoning that any time-shift which might occur as the result of moving
bodies should occur equally in each, because each body moves in equal relation to the
other, I conclude that such time-dilation between moving bodies must be impossible.
An interesting aspect of this argument is that it appears to have been overlooked by
mainstream science texts.
Here is an exercise you can try: Pick up a physics text book that discusses relativity and
see if it covers the ‘Twins’ analogy, or something similar. Or search the
internet for the phrase ‘Einstein twins’. If you find it, see if the authors
also address the above arguments about contradictions in time-dilation. Chances are they
give a lot of double-talk about reference frames; perhaps in the hopes of bluffing the
reader into agreement. Or they make no mention of it, only to label it an enigma and leave
it at that.
Calling something an enigma makes it sound almost romantic, like you should sit back in
awe at the mysteries of the universe and not consider the argument too deeply. But it
should not be called that. It would be better to call it a flaw, a limitation, or
even a mistake in the SR theory.
There’s nothing wrong with having flaws in a theory; many theories have them. But we
should acknowledge such limitations so that better theories may be sought to replace the
ineffective ones. Otherwise students, and even teachers, of science will be stuck with
wrong information and flawed thinking. And such must be detrimental to scientific
progress.
|