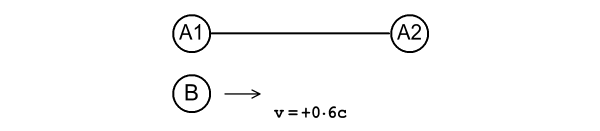Relativity Challenge
Test your thinking skills
This is a challenge designed for
those who still have independent thinking abilities and don’t
automatically believe something simply because some book/TV
science
guru said so. It concerns the Theory of Relativity.
More specifically it concerns the time dilation aspects of Special
Relativity (SR).
The challenge is presented as a set of simple questions which anyone with a
basic knowledge of SR should have no difficulty in following, although
some might have reluctance in answering.
If at the end of this challenge you’ve concluded that something about
the whole SR theory doesn’t sit right… congratulations! You
are at a good starting point for solving the remainder of the puzzle.
Now for the challenge.
The Situation

Fig 1.1
Two accurate identical clocks, A and
B, move with uniform motion along
a shared straight-line path but with different constant velocities such
that the distance between them either steadily increases or steadily
decreases with time. According to the Theory of Special
Relativity, as proposed by Einstein in 1905, these clocks should run at
different rates. To quote:
|
“If
at the points A and B of [the coordinate system] K there are
stationary clocks which, viewed in the stationary system, are
synchronous; and if the clock at A is moved with the velocity v along
the line AB to B, then on its arrival at B the two clocks no longer
synchronize, but the clock moved from A to B lags behind the other
which has remained at B by ˝ t
v2/c2
(up to magnitudes of fourth and
higher order), t
being the time occupied in the journey from A to B.” [1]
|
The Question
We wish to know which clock runs
more slowly. What
information is needed to determine this and how should it be applied?
Rules
Your answer may be expressed in
words, in equations, or a combination
of both. Just so long as it describes which of the clocks
runs more slowly. An answer that does not include this
information will be considered a fail.
Keep in mind there is no acceleration in the system. So
presenting arguments about ‘accelerating reference frames’ or any
aspect relating to acceleration will serve no purpose.
More Details
To assist the challenger, more
details are provided.
What are their velocities?
Let the velocities of clocks A and B be va and vb
respectively. No numerical values will be assigned to these
symbols, however you are free to assign sample values if it will help
in your response. Otherwise these symbols can be included in
equations that describe your answer.
Where are they located?
Let the clocks be located approximately mid-way between our galaxy, the
Milky Way, and the nearest similar galaxy, Andromeda. The
reason for doing this is to minimise the influence of General
Relativity (GR). At the proposed location the gravitational
influence from each galaxy is calculated as being 10 trillion times
lower than Earth’s surface gravity. To remove this tiny
amount of gravity from consideration, we’ll further require the
difference between va and vb be enough such that
SR’s time dilation
predictions exceed those of GR’s. A difference greater than
1% of light-speed will probably be sufficient, i.e. |va-vb|>0.01c.
What are the velocities relative to?
A good question. And also a point of uncertainty in SR
problem solving. So rather than answer that here, it will be
left to the challenger to specify a reference point. Just
keep in mind where the experiment is taking place.
Objections and
Possible Responses
Naturally there will be objections
and it is worth anticipating them in
advance.
Possible response:
It will not be possible to confirm which clock is running more slowly
because no observer can see both at once. The only way to
confirm a difference is if one clock stops, turns around and comes back
to the other clock. This requires acceleration, which in turn
alters that clock’s reference frame and causes time dilation in
accordance with the proper resolution of the Twins Paradox.
Counter response:
Observers are not required to confirm physical events. Either
the dilation occurs or it doesn’t. And if does then you need
to specify which clock experiences more of it.
If you want to say an observer is necessary you should also describe
what types of observers will be suitable. Does it need to be human
or will an animal do? How about an insect or
bacterium? If a human is required, what will happen if humans
become extinct – will relativity no longer apply? And what
about the era before humans existed – did relativity exist?
It’s unlikely that any scientist would insist that the validity of
relativity theory, or any physics theory, requires the presence of life
forms in the universe. Still, given the present state of
science, one can never be sure. So for those who require that
the clocks be compared side-by-side, see parts 2 to 5 of this
challenge.
Possible response:
Each clock will see the other running more slowly, and by the same
degree. This means motion-based time dilation can occur
without having to choose one clock over the other.
Counter response:
Look again at Einstein’s quote. There is no suggestion that
each clock will record less time than the other. A person
responding in this way appears to be describing time dilation as a
perception rather than something real. There are two reasons
why someone might do this. One is to not violate symmetry, as
there is no grounds for preferring a particular clock. The
other reason is avoid the possibility of contradictory experimental
outcomes, since clocks can’t be properly compared at a distance.
But in fact this proposal can lead to experimental
contradictions. See Part 6 for details.
Possible response:
The slower moving clock is the one that has the highest speed relative
to Earth.
Counter response:
Strange as it may sound, this is the explanation behind many of the SR
experiments, such as GPS, atomic-clocks-on-planes, and muon
decay. Although the explanation is seldom worded in this
manner.
Anyone making such a claim is placing Earth at the centre of the
universe and making it an absolute frame of reference against which all
velocities are measured. Outside of geocentrists, we can be
sure few modern-day people do this. Yet that is how much of
SR works.
Also note this experiment is taking place outside the Milky
Way. Are we saying Earth works its ‘relativity magic’ way out
there… that its importance (gravitationally or otherwise) overrides the
influence of billions stars in our galaxy and others?
Further, what if Earth were to be hit by a giant asteroid, broken into
chunks and scattered in opposing directions. Which chunk do
we follow: the largest one, or their collective centre of
mass? Or what if Earth falls into the Sun, is reduced to
atoms, and scattered with the solar wind. Where now is the
universal reference point?
The remainder of this article (Parts 2-5) will run through detailed
examples. It will be focused on determining how much time a
clock records in passing from one reference point to another and back
again. It will show how, even when adhering to the rules of
special relativity, no time difference accumulates between
clocks.
Clock readings will be compared side-by-side so as to
remove uncertainty about readings at a distance. To reduce
the effects of general relativity, experiments are assumed to be taking
place far from gravitational sources and no acceleration will occur
while a clock’s duration is being recorded.
|
Part 2
Two identical clocks – A and B – are attached to rocket
engines. Affixed to the end of each rocket is a very long
pole stretching out behind. The poles are of equal size,
measuring several ‘light hours’ in length (relative to their own frames
of reference), and at the end of each pole is a flag as shown:
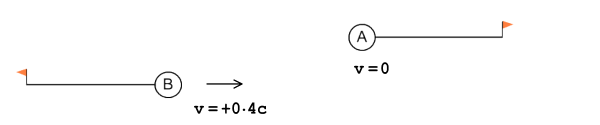
Fig 2.1
Clock A will remain ‘at rest’ throughout the experiment. It
faces left in this diagram. Clock B faces right and comes in
from the left at a constant velocity of 40% the speed of light,
relative to A.
Both A and B carry identical stopwatches. As they pass each
other, each presses the start button on their respective watch.
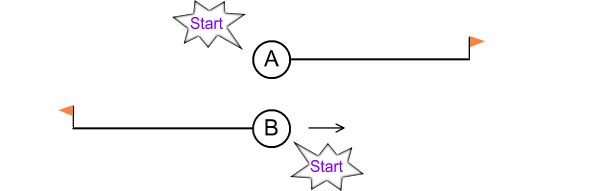
Fig 2.2
B then continues at constant speed. Many hours later, B draws
level with the flag at the end of A’s tail. At this point, B
presses the stop button. It takes note of the reading and
prints it on some paper.
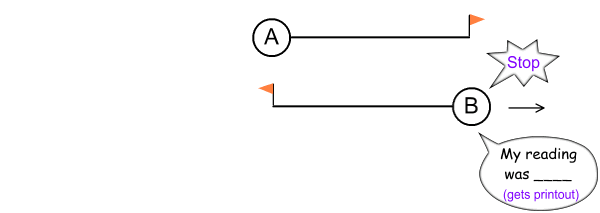
Fig 2.3
Meanwhile far away to the left, and presumably at the same time
(although this can be left as ambiguous for supporters of
‘non-simultaneity’), A draws level with the flag at the end of B’s
tail. At this point, A presses its stop button and prints the
reading on paper.
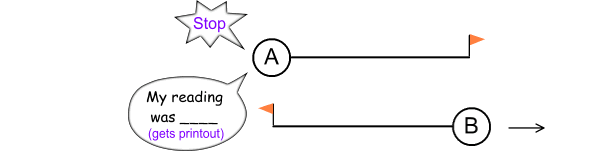
Fig 2.4
A few hours later (allowing time for ‘simultaneity’ to catch up at the
other end, or to compensate for whatever other objections relativists
can think of), B applies the brakes and then reverses all the way back
to A. The two sheets of paper are then compared.
Question: Which printout will show a lesser time: A or B?
There is no wiggle room available here. The situation is
fully symmetrical and each clock moved at 0.4c relative to the
other. And we can’t say the deceleration process will
influence the result because the hard-copy printouts are not going to
change after being printed.
The only sensible conclusion available to a relativist is to agree that
the printouts from A and B show the same time (allowing for
measurement errors).
It should be clear that this situation is identical to the one
described originally, other than it has the poles and flags attached.
So we remove the poles and flags. Now unless someone can find
a valid reason why doing this would now cause one clock to record less
time than the other, especially as the situation is still symmetrical,
it appears no time dilation has taken place.
Calculations:
We’ll do some calculations to go with the above. To simplify
things, change the relative velocity to 0.6c. This gives a
convenient Lorentz factor of 0.8.
Set the length of each pole at one light hour (60 light minutes) long,
as measured in its own frame of reference. How do we define
this length? There is a mirror attached to A’s flag, and when
A fires a laser pulse at the mirror it (A) notes the signal takes two
hours to return. B likewise has a similar laser/mirror setup to confirm
its length as 60 light minutes. (This is similar to how we measure the
Earth-Moon distance.)
As noted earlier, each stopwatch will record the same time
elapsing. What will that time be? According to
classical mechanics, 60/0.6 = 100 minutes will have elapsed.
But let’s give relativity benefit of doubt and say (e.g. due to length
contraction) it is 60/0.6*0.8 = 80 minutes.
Note 1: For those who disagree with the time of 80 minutes, feel free
to insert any number you want. Just be sure to put the same
reading on both stopwatches because symmetry requires it.
Note 2: As with the previous example, the events occurring at both ends
of the poles can either be considered as taking place in the same time
frame or different time frames. Here we are only interested
in how much elapsed time shows on each stopwatch.
Perspective
In order to represent the situation more fairly we need to show
perspective. According to the rules of length contraction
each clock will see the other pole 80% shorter than what the clock
mounted on the same pole will see. That is, each clock sees
the opposing pole being 48 light minutes long. In other
words, A sees this:
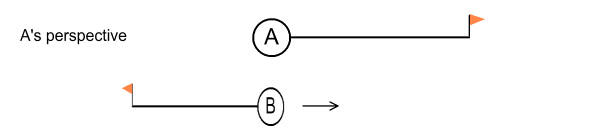
Fig 2.5
And B sees this:
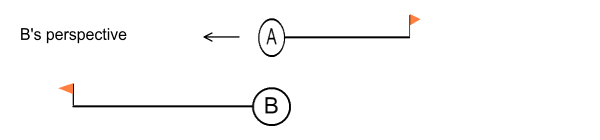
Fig 2.6
So each clock sees the other pole 80% shorter and each clock records 80
minutes as it passes from one end to the other.
Note: for visual clarity, the contractions shown are 70%.
Part 3
This next part will examine a ‘reverse perspective’.
Two observers A1 and A2 sit at either end of a pole measuring 60 light
minutes (in their own frame of reference). Coming from the
left is another observer B moving right at 0.6c (relative to A1 and A2).
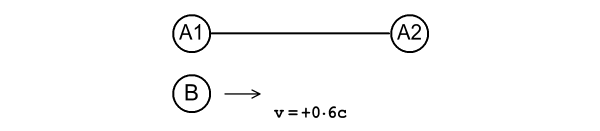
Fig 3.1
As discussed, B will observe 80 minutes passing as he moves from A1 to
A2.
Now suppose B had a special ability of making himself invisible at
will. Initially B is invisible while at the left of
A1. When B passes A1 he makes himself visible; and when
passing A2, makes himself invisible again. This is how the
passage would look without showing contraction.
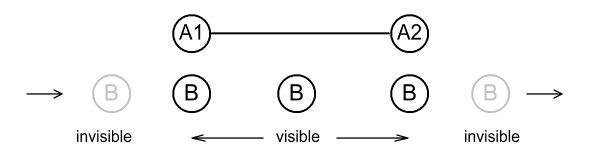
Fig 3.2
Note 1: for convenience the invisible periods are shown in grey.
Note 2: instead of invisibility we could say B raised a flag when
passing A1 and lowered it when passing A2.
We will now look at the situation from the perspective of A1 and
A2. A1 will see this:
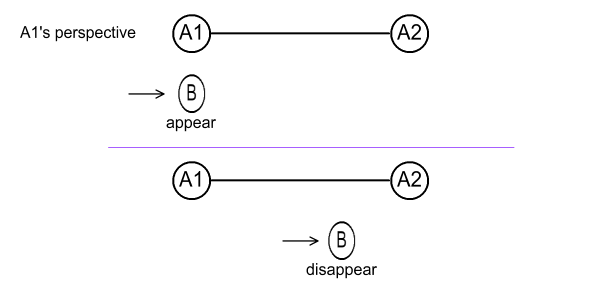
Fig 3.3
A2 will see this:
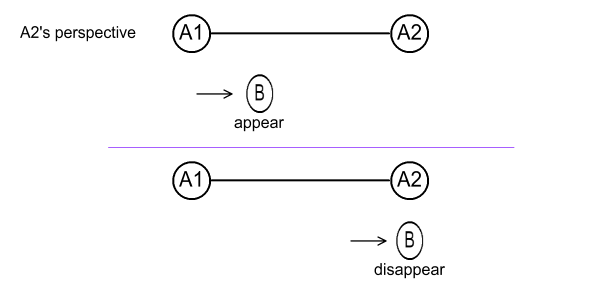
Fig 3.4
Due to length contraction, A1 will see B shrunken along its length and
closer. B’s starting position will be level with A1 but its
ending position, where B disappears, will be 80% of the A1-A2 distance.
In a similar manner A2 will see B closer (to A2). But this
time B’s ending position is level with A2 while its starting position
is 80% of the A1-A2 distance.
The above may seem odd because B doesn’t disappear until it sees itself
drawing level with A2. But since B is in constant motion and
never slows down relative to A1, A1 will see its position
contracted. At all times, B appears only 80% of the distance
that it should be at according to classical mechanics. So
when B passes A2, A1 still sees B at the 80% mark. The
reverse is true from A2’s perspective, in that A2 always sees B closer
to its end of the pole by an 80% contraction factor.
How much time does A1 observe B taking from its start position to where
it becomes invisible? Looking at the perspective diagrams,
the answer is 80 minutes.
Part 4
We’ll now extend the above to a three clock/observer situation.
As before we have A1 and A2 sitting either end of a 60 light minute
pole. B comes in from the left at 0.6c, and makes itself
visible as it passes A1. At that point, both A1 and B press
the start button on their respective stopwatches.
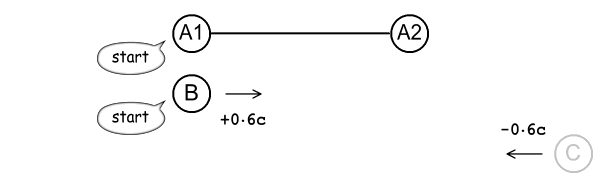
Fig 4.1
Coming in from the right is another observer C (see above
diagram). C has its own stopwatch and is invisible while at
the right of A2.
C moves left at 0.6c, relative to A1-A2. The experiment is
arranged such that A2, B, and C will see each other draw level at the
same time.
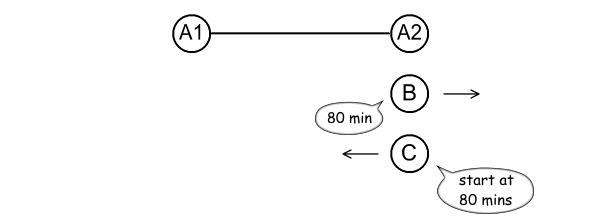
Fig 4.2
At this point B becomes invisible and C visible. B announces
its elapsed time (of 80 minutes), and C sets its stopwatch to start
with B’s reading.
From the point of view of A1, and showing perspective diagrams, this is
what A1 sees of the B/C meeting:
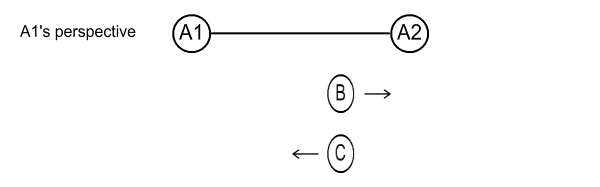
Fig 4.3
That is, A1 sees B and C draw level at same location, and at a distance
80% of the way from A1 to A2. The reason for this identical
location is that the length contraction formula (the Lorentz transform)
squares velocity, which makes its direction unimportant. And
since B and C have the same speed relative to A1 (of 0.6c), they get
the same length contraction treatment. *
Because of this, the time A1 observes for B to reach the B/C meeting
point will be 80 minutes. A1 however leaves its stopwatch
running. From the perspective diagram we can see that the
time C records passing from the B/C meeting point back to A1 will also
be 80 minutes.
When C finally reaches A1, both A1 and C will have ticked off 160
minutes in total.
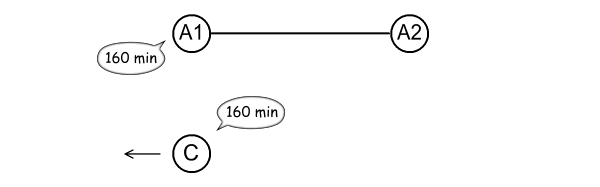
Fig 4.4
* For those who doubt A1’s perspective and believe A1
should see B and C
meeting when level with A2, redo the experiment but this time eliminate
the pole and A2. We can also dispense with the invisibility
tricks.
Everything else remains the same.
B passes A1. 80 minutes later (in B’s frame), B notices
itself drawing level with C. This will be what A1 sees of the
meeting:
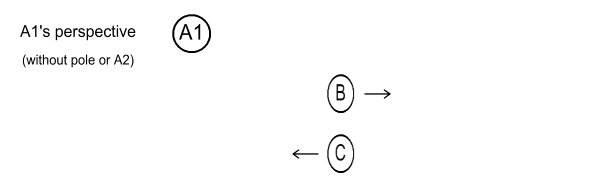
Fig 4.5
Since
A2 and the pole are no longer there, A1 can only judge the crossover
occurring 48 light minutes away rather than 60 light minutes.
Both B
and C’s position contracts by the same amount (80%) because both have
the same speed relative to A1. |
Part 5
Now for the final example involving a science-fiction scenario with
space travel. This example describes the ‘Twins Paradox’
scenario, i.e. the passage of a traveller from Earth to a distant point
and back again.
We’ll take the situation from Part 4 and make changes to it.
. Increase the length of the pole to 6 light years (relative to A1-A2).
. Replace A1 with Earth
. Replace A2 with an alien planet, which we’ll call ‘Planet X’ or just X
. Replace B with a spaceship
. Replace C with another spaceship
. Finally, delete the pole!
Using the same calculation methods we can determine that time recorded
by B in travelling from Earth to X will be 8 years. B then
transfers this reading to C which adds to it on the way back:
Here’s a non-perspective sequence of the events:
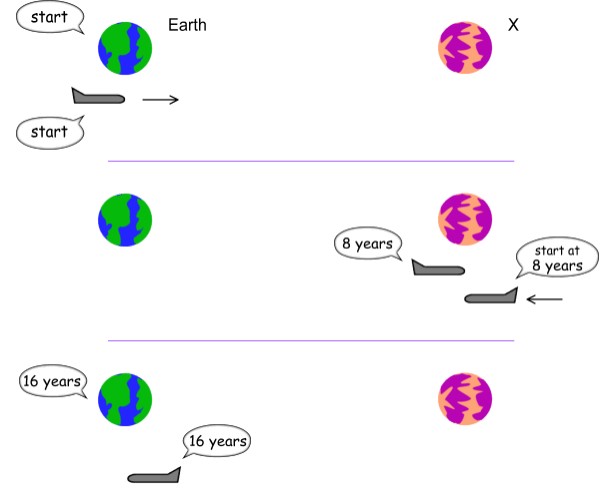
Fig 5.1
And here’s a perspective drawing showing Earth’s view of the B/C
meeting:
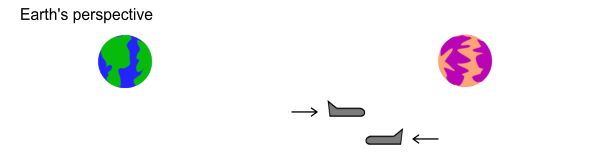
Fig 5.2
As can be seen, the total time recorded by Earth between the departure
of B and the arrival of C is 16 years. And the total of times
recorded by B and C add up to 16 years.
The only difference between this and the traditional Twins Paradox
story is that we have used two travellers. The reason for
this was to exclude acceleration from the scenario. However
if acceleration were not a factor in determining time dilation, as some
say it isn’t, it should be clear that the same outcome would happen for
a single traveller. Otherwise, the entire amount of time
dilation (as described in the traditional Twins Paradox story) would
need to occur during the brief reversal at the far end (because the
traveller would trail a fixed distance behind C and thus need to sync
with C on the return journey).
Part 6
This section covers the claim that the two clocks in the original scenario
(Part 1) will each see the other running more slowly.
A 2 light-hour-long pole is located in space, with a flashbulb in the
centre. Two spaceships approach from either side,
each travelling at the same constant speed relative to the pole. Each
ship carries an accurate atomic clock that can be operated as a
stopwatch.
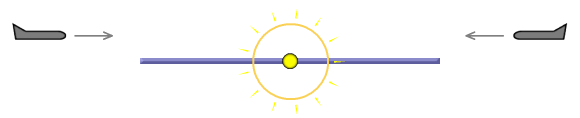
Fig 6.1
The flashbulb goes off and the leading edge of its pulse takes exactly
one hour to reach each end of the pole. By coincidence, each
ship encounters the pulse just as it passes its end of the
pole. At this point both ships press the start button on
their respective stopwatch.
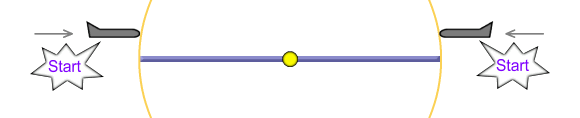
Fig 6.2
As can be seen, the situation here is perfectly symmetrical.
If the question was asked “which clock will run more slowly?”, there is
no logical way of choosing one over the other. The relativist
however could reply that each sees the other running more slowly, or
running more quickly.
In the original situation a suggested response was that each clock
would run, or appear to run, more slowly than the other.
There the clocks were moving apart, here they are moving
together. Does that mean they should both run faster here?
An important point about time dilation is that it is
non-directional. The Lorentz Transform squares the velocity
and this removes any directionality from it. So to be
consistent the answer would need to be is that they are both running
slower. Not that it is important for the argument here, but
we’ll stick with ‘both running slower’.
So as the spaceships move together, they can each say the other ship’s
clock is running more slowly than its own. This creates an
inevitable dilemma. Because at some point the spaceships are
going to pass each other, where the flashbulb is. At this
point they will stop their clocks and make a comparison. If
the time dilation being described was real rather than a perception,
this requires that each clock must show more elapsed time than the
other!
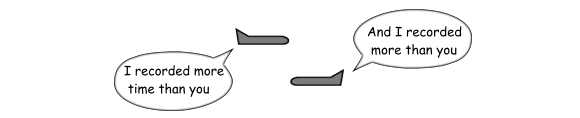
Fig 6.3
As this is not going to be possible, and since motion-based time
dilation is non-directional, we must likewise reject the notion that
the clocks in the original situation were each running slower or each
running faster than the other.
|
Epilogue
An important point has been overlooked in the above. In Part
2 we calculated clock A would experience 80 minutes traversing the
length of B’s pole, and vice-versa. The times were the same
but didn’t agree with the classical (Galilean) calculation of 100
minutes. Similarly in Part 5, the ships covered a distance of
12 light years but did so in less time than they should have,
classically speaking.
The above seems to indicate that time dilation might be possible but
only if all parties agree on the same amount. That is, if all
parties slow down by the same degree.
How could that be? If time dilation occurred equally at both
ends, and A reached B’s flag in less time than it ‘should have’, how
would B know the time was less, since B likewise recorded less
time? For that matter, if all parts of the universe
slowed down (or sped up) by the same degree, how would we know time
dilation is occurring at all?
The confusion here comes from the definition of velocity.
When we speak of velocity we normally talk about how far something
moved in a unit of time. The definition of velocity, or
rather speed (velocity includes direction), is distance travelled
divided by time taken (D/T). This is a useful definition and
nobody has confusion with it when applying it to classical mechanics
situations.
Relativity though is a different ball game. In relativity we
compress and expand distances and times. In relativity,
‘distance divided by time’ becomes ambiguous. What ‘distance’
and what ‘time’ – the classical or relativistic? In the above
examples we mentioned velocities of 0.6c – whatever did that mean?
Definitions are important. So in order to remove ambiguity
let’s make it clear. Speed refers to the round-trip-distance
divided by the round-trip-time as seen by the observer at a combined
start/end location. There are other ways of describing speed
but the advantage of a round-trip is it removes uncertainty about
timing at a distance.
To give an example, say a rocket departs Earth and visits a star
located 10 light years away, as measured by standard astronomy
methods. It returns 30 years later, as measured by those on
Earth. This rocket travelled a total distance of 20 light
years and took 30 years to do it. Therefore its average speed
was 20/30= 0.66c.
Applying this to the situation in Part 4, the B/C observer combination
travelled a distance of 120 light-minutes in 160 minutes.
They therefore had a speed of 120/160 = 0.75c. In
Part 5, the ships covered 12 light years in 16 years, making their
speed 12/16 = 0.75c.
So that’s the mystery solved. The ships/observers were never
going at 0.6c, they were going 0.75c. We just labelled their
speed wrongly. Once we specify the correct speed, the times
taken will exactly agree with Galilean predictions.
Here’s the problem. When relativists make a statement like:
“The ship is moving at 90% the speed of light.”
They seldom pause to consider what that means. All they know
is what it’s relative to.
Properly speaking what it means is that an object will travel 90% of
the distance that light would in a given time span, where distance and
time are measured in classical terms according to what the velocity was
‘relative to’.
But relativists are not known for thinking, only for reciting
theories. They take the number 0.9c and starting plugging it
into equations. If the results of those equations determine
that the ship moved a different distance in that time span, then the
ship was not moving at 0.9c, it was moving at some other
speed. Otherwise we are abusing definitions and ‘velocity’
has no meaning.
Thanks for coming
This concludes the
challenge. There are no prizes for ‘solving’ it,
sorry. Its purpose is to be thought-provoking and hopefully
you found it so.
I’d like to thank the late Professor Herbert Dingle for the
inspiration. Dingle was a former expert and author on
relativity who originated a similar challenge in the 1960s and used it
to query many of the establishment leaders. Needless to say
it provoked some interesting reactions. His story is worth
reading and can be found online here [2],
and the appendix is here [3].
For the next step in the puzzle, proceed to Part 2 where acceleration
and gravity is discussed:
Relativity Challenge - Part 2
(<-- click to read)
[1]
http://www.fourmilab.ch/etexts/einstein/specrel/www/
[2] http://blog.hasslberger.com/Dingle_SCIENCE_at_the_Crossroads.pdf
[3]
http://blog.hasslberger.com/docs/Dingle%20Appendices.pdf
|