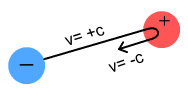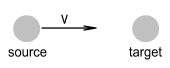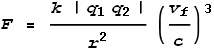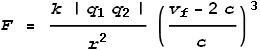Electric Fields
Much has been said in the preceding chapters about something called the
electric field and how it is responsible for things like electrical and
magnetic forces. So what actually is an electric field?
Putting aside equations, the general definition is along the lines: “a
region of space surrounding a charge where another charge experiences a
force”.
Stated like this, the field sounds like an abstract notion, almost like
a mathematical concept that serves no purpose other than to enable one
to calculate forces. Or perhaps it describes an altered
property of empty space. If so, this would appear a
contradiction since empty space should have no properties.
Static or flowing?
Is an electric field something that stands still or something that
flows? In general, a field that doesn’t change its intensity
is described as ‘static’. A field that fluctuates in
intensity might be described as ‘dynamic’, but not flowing as
such. Is that an accurate description?
We know that the effects of an electric field propagate at a finite
speed – that of light. If we could suddenly introduce an
identical charge nearby another, the existing charge would not respond
immediately. Instead there would be a brief pause before the
existing charge began accelerating away. This would seem to
indicate there is something physically moving from one charge to the
other and then striking that second charge with a force.
But then again, a scientist might argue that there is nothing moving
between the charges. Instead, what we observe it is just the
effects of ‘relativity of simultaneity’. By this he means, it
takes a while for the presence of a charged particle in one location to
become true at another, and this delay in presence is determined by
distance and the speed of light.
Such explanations can be confusing and quite contrary to our common
sense. As a scientific principle, it is always best to
consider logical explanations before turning elsewhere. By
‘logical’ we mean something that can be modeled and understood in terms
of other processes, particularly those at a larger scale.
Let’s take a river as an example. Is a river static or
flowing?
If we view a river from high above, all we see is a fixed body of
water. Just a line on a map and we would probably describe it
as static. When viewed from ground-level, the picture is not
much different. If the water contains no debris and no
turbulence, the river gives no indication of its underlying nature and
might still be described as static.
If we throw something into the river like a leaf and see it float
downstream, at that point we might suspect the river itself is also
moving with the leaf. But then again, a scientist might argue
“No, the river is standing still. The leaf moves because the
water applies a force to it.”
But of course no scientist would seriously say that. We know
perfectly well that the river is not static at all. The water
is flowing and that is what pushes the leaf along.
Could an electric field be a similar phenomenon? Could what
we describe as an electric field be in fact, not just be an abstract
mathematical entity, but an actual flow of material that moves outward
from a charge and imparts a force on other charges when it hits them?
On one hand this sounds logical because it explains why there would a
delayed effect if the ‘material’ moved at the speed of light.
It would also explain how an electric force is exerted at a
distance: it isn’t, the force is applied directly when the
material meets/hits the other charge.
On the other hand it sounds illogical because the material is not
coming from anywhere. It flows out of the particle, yes, but
without first coming into it from somewhere else.
So what if the electric field ‘material’ was not coming from elsewhere
but being generated ‘on the fly’? That is, it was
continuously being produced and then ejected?
This would seem impossible because it violates conservation
laws. As we know, quantities like mass and charge are
conserved and can’t just be created anew. At least not
without being created in neutral positive/negative pairs (in the case
of particles) or converted from other forms (in the case of mass).
But note that the electric field material described here contains no
mass or charge. So a continual creation of this substance,
whatever is was, would not violate any known conservation
laws. The only thing it would do is apply a continual force
on another charge standing in its path – something we observe as
true. Therefore the process could continue forever without
increasing the amount of ‘normal matter’ (subatomic particles) in the
universe.
For the sake of description let’s call this material ‘field substance’
and state the above as a hypothesis.
The Electric Field Hypotheses:
Each charged particle generates something called ‘field substance’
which makes up what we call an electric field. This substance
is continuously and perpetually generated within charged particles and
moves away at the speed of light (relative to the particle).
As it spreads spherically outward it becomes thinner and
thinner. This substance is a not a mathematical abstraction,
but an actual physical substance that travels through space.
When it strikes another charged particle it exerts a force.
The amount of force and its direction will be based on charge values,
local field substance density, and relative velocities.
Analogies
In order to visualize what is being described it is best to make some
analogies. There are a number of ways of thinking about
this. One is to imagine a series of rubber balloons that
start at the surface of a (spherical) charged particle and expand
outwards. As they do, they become more and more stretched,
but never burst.
Another way is to a imagine a fine mist of particles being sprayed
outward. As they do, their density becomes less and less
dense, which means fewer will hit a target further away and thus exert
less force.
These animations should explain what is meant.


Left: a series of rubber balloons, representing ‘field substance’,
form at the surface of a charged particle and expand outwards, becoming
increasingly thinner but without ever bursting.
Right: tiny particles are being generated within a charge and ejected
at the speed of light.
These are just analogies, mind. Perhaps it would be more
accurate to describe a continuous, infinitely-stretchable lump of
rubber. But that is difficult to draw.
For various reasons, the second method of imagining the field to be
made of tiny particles will be the most convenient model to work
with. That doesn’t mean it is correct, just that it is the
simplest way of imagining the interaction between field and
charge. In this way we can consider the particles as
ballistic projectiles that exert a force on a target. Another
thing that should be obvious from this is that the density of particles
will decrease with inverse square of distance, thus bringing their
impact force in line with the Coulomb force. This is because
they are evenly spread over the surface a sphere whose area increases
with distance squared.
Perhaps the simplest direct analogy for this ballistic particle model
would be the solar wind coming from the Sun, and how the wind exerts a
force on objects such as ‘solar sails’ (which are not reality as yet).
Field lines
Quite often electric fields are described and drawn in terms of lines
that come in and out of, and curve around, charged particles.
While such drawings can be useful, it is important to remember that
they are only concepts for showing force directions and don’t
necessarily represent anything physical.
Unfortunately this has led to major misconceptions in our understanding
of fields.
Consider this electric field diagram:
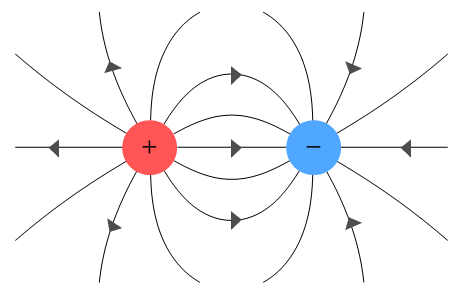
This oft-cited presentation shows a positive and negative charge. The
field starts at the positive charge and moves outward. There are no charges on its left.
So the field moves away in mostly straight lines (with the left-most line being exactly
straight) and steadily weakens with distance. To the right is a negative charge. So the
field bends its way toward that charge and disappears into it. Meanwhile there is nothing
to the right of the negative charge, so a field seems to appear from nowhere and move
toward that charge.
This concept is surely wrong. An electric field could not bend toward another charge
because the field doesn’t know where that charge is before it gets there. When we walk we
can see ahead and use that information to decide our direction because our sight is much
faster than our legs. But an electric field is already moving at light speed and cannot
‘see ahead’ any faster than it is moving. Additionally, the field should be
shown running in both directions because the positive-negative distinction is arbitrary.
A more accurate version of events would be in this diagram:
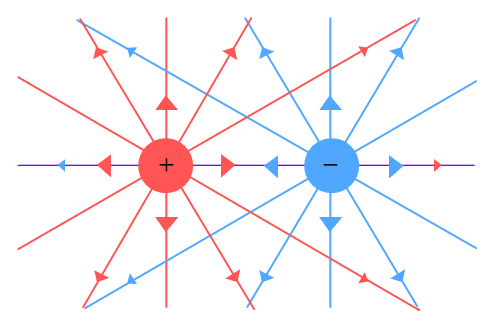
Here we see both charges generating a field, and both fields extending
directly away from their charges, in straight lines, and weakening with distance. The
previous diagram may be accurate if it were describing the net force experienced by a
nearby separate positive charge, but not as a general field-line diagram.
Modelling the forces
When electric field strikes a charged particle it exerts a
force. On an intuitive level this makes sense. If
we were to spray a material substance, such as a jet of air, at an
object we would exert a force on that object and it would be pushed
away.
But with charged particles the direction of force is not always
intuitive. There are two types of interactions we are dealing with: the
repulsive force between like charges; and the attractive force between
opposite charges. In trying to understand how things work at
a ‘too-small-to-see’ microscopic level, it is useful to make
comparisons with things at an ‘everyday-world’ macroscopic level.
For the repulsive force this is easy. Imagine a stream of
tiny bullets emerging from a charged particle. These bullets
emerge from all directions and travel directly away from the particle
at light speed. A similarly charged particle nearby would
feel the force of these bullets and be repelled by them. The
closer the second particle was to the first, the more bullets would hit
it, and hence the force would be greater. If the particle was
further away, fewer bullets would hit and the force would be less.
In keeping with the Velocity Dependent
Coulomb’s Law (VDCL) discussed
earlier, as the particles moved inward, the impact speed of the
bullets, and hence the force, would increase. As the
particles moved outward this would lower the impact speed and
force. And if that second particle moved away from the first
at the same speed as the bullets (i.e. at light speed), then the
bullets would not hit and hence could apply no force at all.
So what analogy could we make for the attractive force? Again
this looks easy. Simply reverse the direction of the bullets
so that they dive inward toward the charged particle.
Unfortunately there are major problems with that idea. In
order for the bullets to move toward the particle they would have to
know in advance, not only the position of the particle, but also its
velocity. They need to know the particle’s velocity because
the bullets must strike that particle at light speed. The
bullets would also need to emerge at the beginning of time, from the
furthest reaches of the universe, and somehow affect other particles in
reverse order – i.e. impact particles closest to their destination
first. This involves a level of clairvoyance and inverse time
travel far beyond what any sane scientist would consider
feasible. Obviously this model is wrong and we need a
different approach.
A new model of electric forces
In order to explain the interaction between of oppositely charged
particles, we can look at electric fields and forces as follows:
Each charged particle emits a field type corresponding to its
charge. Positively charged particles emit a ‘positive field’
and negatively charged particles emit a ‘negative field’. The
field itself however contains no charge, just information about the
charge it originated from. So we can describe the field as
having a ‘sign’, i.e. positive or negative.
These fields emerge from all ‘sides’ of the particle and move directly
outward at exactly light speed relative to their starting
point. When they meet another particle one of the fields will
interact with it, either pushing or pulling, depending on that
particle’s charge.
How do these fields interact? We already have a simple
analogy for the pushing process, so let’s now look at the pulling
process. The field emanates from the charged
particle and moves away from it at light speed. When it hits
an oppositely charged particle, the field can be considered as making a
sudden ‘U-turn’ and pushing that particle in the opposite direction,
i.e. pulling it. The pulling action happens at light speed
and that particle receives the same (but opposite) force as a
like-charged particle would from the same field. This diagram
represents the action:
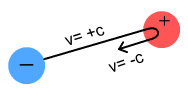
For an analogy, consider a paddle steamer. As the big boat
steams along the river, its paddles reach out and pull the water in the
opposite direction, much like a swimmer’s hands. Now suppose
this old-style boat had been equipped with a modern, stronger propeller
engine that was able to move the boat in either direction.
If the propeller were to pull the boat backward, the force of the
paddles on the water would increase. If the propeller were to
gently push forward, the force of the paddles on the water would
decrease. If the propeller pushed at the same speed
as the paddles, the paddles would exert no force on the
water. And if the propeller pushed even faster, the paddles
would now begin to push against the water.
Okay so there are no bullets or paddle steamers at the atomic
level. These are just models to help us visualize what’s
going on. However there is a separate point to this;
especially the pull-field U-turn model, which will be made use of in
the next section.
Field Velocity
Time to introduce a new concept: Field Velocity. When charged particles
interact it is not the particles themselves that pull or push on each another, rather it
is their fields. The Velocity Dependent Coulombs Law (VDCL) tells us to look at each
(source) particle’s velocity and then, depending on the charges, add or subtract this
velocity to the speed of light to determine how much impact it will have on another
(target) particle. This net velocity is then cubed to determine the degree of force
applied.
Since the target particle only interacts with a source particle’s field however, it
makes more sense to talk only about this net velocity of the field. This velocity, herein
called the Field Velocity, is defined as the velocity at which an electric field strikes a
target particle. In a situation where a source particle is moving at velocity v
toward a target (see below diagram), the Field Velocity vf
will be:
vf = c + v
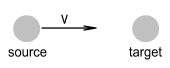
This new velocity vf will be greater than
light speed c if the source is moving toward the target, and less than c
if moving away from the target. Importantly, this velocity vf
is defined the same way for both like and oppositely charged particles.
Using Field Velocity in the VDCL
Now that we have defined Field Velocity we can use it in the VDCL
equation. But instead of having a single equation we’ll have a separate one each for
‘push fields’ and ‘pull fields’. Here they are:
VDCL for Push fields:
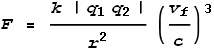
VDCL for Pull fields:
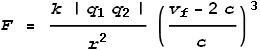
Here are some points to note:
When the particle velocities are zero, i.e. at rest relative to each
other, both equations become the same and equal to Coulomb’s Law.
The signs on the charges are not important in the equations because we
choose which force equation to use based on the charge signs. Thus only the absolute
values of the charges appear in the equations (between the “|” symbols).
For both equations, a positive result means repulsion and a negative
result means attraction. Hence it is possible for a ‘push field’ to pull and
vice-versa. Although this will only happen for particle velocities above light speed.
The only difference between Push and Pull is that Pull contains a -2c
term. This represents the U-turn made by a ‘pull field’ when it meets a target
particle: the field reverses its direction at double the speed of light relative to its
incoming speed. This is the same thing as you would have in a car U-turn: in order to be
eventually moving backwards at the same as your forward speed, your net change in velocity
must be the negative of double your incoming velocity.
You may be wondering what the point is in having separate equations (and
making things more complicated!). The reason is partly because it better represents the
field models above. But a more important reason for this will become clear in a later
chapter about ‘sideways forces’.
A correct representation of magnetic fields
Some final points before moving ahead. I wish to a correct a common
misrepresentation of magnetic field lines. Magnetic fields are often drawn as circling a
wire. A diagram of such looks like this:
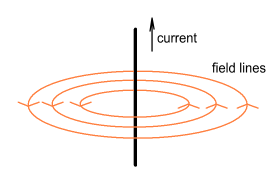
In this diagram the magnetic field lines seem to start at various
distances from the wire and then proceed to circle it at fixed radii. There is also
usually a picture (not included) of a hand beside the diagram showing a ‘thumbs
up’ to tell you about the right-hand rule. The implication of this diagram is that
magnetic force acts at right angles and would force something to circle the wire.
But this is clearly untrue. When two current carrying wires are placed in parallel, the
only force between them is either directly toward or directly away from each other. The
wires are never pushed sideways, as if to orbit each other as the diagram implies; nor
could they be. If a force is caused by a wire then that force must come from
that wire. In other words we wouldn’t expect a force to appear at a certain distance
away and then travel sideways. Here is a more realistic representation showing the force
lines moving outward:
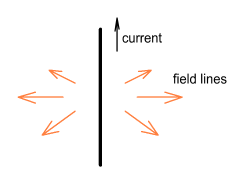
Similarly, the force lines from a coil of wire are also misrepresented.
They show the field lines emerging from the centre of the coil, when there is nothing at
that centre for the field to emerge from. Again the actual field must come from the coils
itself. Here is a before and after correction diagram:
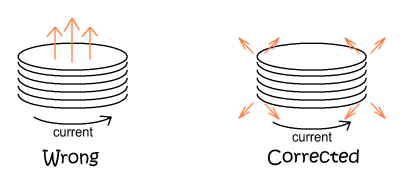
The net force may feel like it’s coming from the centre, but
it’s really coming from the wire all around it. A simple experiment involving an
electric coil hovering over a paperclip shows the clip being attracted to the edge of the
coil and not its centre. In fact, for a large diameter coil, the force at its centre is
particularly weak.
Conclusions
Electric fields are commonly described in an abstract manner that does
not explain how or why charges interact at a distance. But by
considering the electric field as physical substance we can describe a
model for how the electric force takes place, why it varies with
inverse square of distance, why its effect is delayed, and why the
force appears to vary as a function of relative velocity.
|