Relativity Challenge – part 2
Dealing with acceleration and gravity

In the previous chapter we looked at a number of situations in which
clocks moved at different constant velocities but without experiencing
gravity or acceleration. There it argued it was possible to
construct scenarios where one could not favour one clock over another,
in terms of having one experience more time dilation. It
ended up applying these scenarios to the traditional ‘Twins Paradox’
story and concluded that they should have the same age upon return.
In this chapter we’ll do the same but this time include the effects of
gravity and acceleration. It will make reference so something
called the Principle of Equivalence. The details of this
thought experiment may seem overdone but they are required to counter
the many possible objections that might arise from Special and General
Relativity (SR and GR) supporters.
The Situation
In the first preliminary step we take Earth and relocate it far into
intergalactic space. It will be far enough out such that
gravity from the nearest galaxy is a trillion times less than Earth’s
surface gravity. The reason for doing this is firstly so that
we don’t need to consider the gravity of surrounding stellar bodies,
and secondly to remove the motion of the Earth around the Sun and Milky
Way from consideration.
Next we prevent the Earth from rotating. Likewise we do this
to avoid having to consider the SR/GR effects of the rotation speed and
the small amount of centrifugal force it provides.
Now to begin the story.
A rocket sits on the Earth’s surface with a large supply of
fuel. Inside it is a room with living facilities and enough
food and oxygen to support an occupant for many months. It
also contains an accurate atomic clock. Beside the launch pad
is an identically-fitted room. It contains a similar clock
that has been synchronised with the one aboard the rocket.
There is also a third clock on the opposite side of the Earth that is
synchronised with the other two.
Two identical twins agree to take part in the experiment.
Each will spend the next several months either in the rocket or the
Earth room, but neither will know which. Prior to launch,
they are both given a sedative and put to sleep. Each twin is
then randomly assigned to be moved into either the rocket or the
stationary room.
The rocket lifts off. At first, very slowly so as not to
apply much acceleration. Then as it moves further from Earth
and gravity decreases, the rocket increases its acceleration to ‘fill
in’ what is missing from Earth’s gravity. This acceleration
will be steadily increased so that the gravity felt at all times will
be exactly equal to 1G. That is, the gravity measured by an
on-board accelerometer (as the sum of real plus artificial gravity)
will measure the same as on Earth. Assume that the rocket
engine is silent and acceleration is smooth.
Shortly after launch, when the acceleration has steadied to 1G, the
twins wake up. Neither of them know which room they are
in. The rooms are identical in layout and both experience
what appears to be gravity. If they drop something it will
accelerate toward the floor at 9.81m/s2, i.e. at 1G.
Now according to the Principle of Equivalence (also called the strong
equivalence principle), as proposed by Einstein and frequently
described in terms of falling elevators and rising rockets, the
situation inside the two rooms is essentially identical. That
is, there is no experiment you could devise that would allow either of
the twins to determine which room they are in. We will also
assume the rooms are not very tall. This is to prevent an
occupant in the Earth-room from measuring slightly less gravity near
the ceiling.
Question: According to the combined rules of SR and GR, will
one of the clocks be ahead of the other, and if so, what is the reason
for selecting that clock instead of the other?
The fact that the clocks are moving away from each other means they
must somehow have different velocities, otherwise they would remain a
fixed distance apart. Therefore according to SR, time
dilation should be occurring and the faster-moving clock should be
running more slowly. But since the relative speed between the
Earth and rocket is at all times exactly equal from both viewpoints,
there appears to be no way of determining which is ‘faster’.
As for GR, since the acceleration-slash-gravity situation of both rooms
is exactly equal at all times (other than the brief lift-off),
according to the Equivalence Principle it would appear we are also
unable to favour one clock over the other.
So we are left with a conundrum: either we find a way of favouring one
clock over the other or we agree that no time difference accumulates
between then.
Now an objection might be that we have no way of comparing the clocks
without one of them stopping and reversing, which would destroy the
symmetry of the situation. And so the question of which of
them runs faster up until that point is somehow hypothetical or
meaningless. But this avoids the issue because the question
here is about which clock according to the theory of SR and GR, runs
slower. Unlike the ‘Copenhagen Interpretation’ of quantum
mechanics, relativity does not depend on observers to determine the
reality of a situation. So the answer to this question won’t
depend on the clocks ever being compared or not.
Still, this objection can be overcome and will be addressed in the
remainder of this essay.
After travelling for 10 months, and using a simple classical mechanics
calculation, we could determine that the rocket is moving at 87% the
speed of light (relative to Earth, which is now relocated outside our
galaxy). At this speed we get a Lorentz factor of
2. This might mean that either the rocket or Earth clock is
running half the speed of the other. These numbers however are
not so important because we mainly care about which clock is ahead of
the other, and not by how much (although we are also interested in
that!). So let’s just pick 10 months as an arbitrary duration
and assume a rough Lorentz factor of 2 at that point. This
factor will be sufficient to override minor clock-drift errors,
measurement errors, and brief periods where the acceleration of the
rocket is not 1G, such as the launch and rotation (as described
later). It should also cause noticeable differences in what
the twins remember about the duration of their journey, assuming that
one is ‘running’ half the speed of the other.
So after travelling for 10 months (according to the local clock) the
occupant aboard the rocket will take a sedative. The same
will occur at the Earth-room (according to their clock). Both
twins will then sleep for a while. The rocket engine will
then be stopped, allowing the craft to drift freely in space with no
acceleration. It will then be gently rotated 180 degrees to
face the opposite direction – now pointing at Earth. The
engine will then be started again, applying an acceleration force of
exactly 1G. Both twins will then wake up.
When the rocket-twin awakes, he notices no difference. Just
as before, he experiences what feels like a gravitational force of 1G
toward the floor. The Earth-twin experiences the
same. The rocket is facing the opposite direction and is now
decelerating, but by all accounts everything according to the
Equivalence Principle is the same. There is still no
experiment either twin could perform to determine which is experiencing
gravity.
Therefore it would seem that according to GR, both clocks should still
be running at the same rate. And since the relative velocity
is still identical – that aspect never changes – the clocks’ situation
is still symmetrical according to SR.
An objection here might be that there is a difference because the
clocks are experiencing ‘gravity’ in opposite directions. And
therefore the clock on the rocket will now be faster or slower (pick
one!) than the one on the Earth. For those who raise this
objection, refer instead to that third clock placed on the other side
of the Earth. It is still in-synch with the first Earth clock
and now experiencing gravity in exactly the same direction as the
rocket.
To continue the story, the deceleration process continues for the same
time as the original acceleration process (10 months), at which point
the rocket comes to rest relative to Earth. However the
engine doesn’t stop. Instead it continues to apply exactly
the same amount of force. Deceleration becomes acceleration
and the occupant notices nothing unusual.
The acceleration continues for the next 10 months (according to the
local clock) until the rocket reaches (presumably) the original
rotation point. At this point (according to their own
clocks), both twins are put to sleep, the rocket is rotated 180
degrees, and then starts to decelerate while pointed away from
Earth. Both twins awake and notice nothing unusual in their
‘gravity’ situation.
The rocket continues its deceleration in a perfect reverse of its
original departure, steadily coming to a stop relative to Earth, and
all the while carefully adjusting its acceleration to give an on-board
experience of 1G. Just prior to landing, both twins are put
to sleep and then awoken after landing.
The rocket has now landed beside the replica Earth room.
Neither twin has yet to emerge, and neither still has any idea which
one of them was aboard the rocket.
Not that it matters. This story was never about the twins, it
was about the atomic clocks. The twins were just there to
make it interesting and to bring it in line with the historical thought
experiments such as falling elevators and the ‘Twins Paradox’.
So to state the obvious question: allowing for minor clock-drift errors
and the brief periods of launch, landing, and rotation, when the clocks
are compared side-by-side, which of them will have recorded more
time? And why not the other way around?
And while we’re at it, which of the twins will be older?
Discussion
Now that the story has been told, it’s worth anticipating with what
objections might arise. Several things can be predicted about
how relativity supporters will handle this:
1. They won’t accept the twins could be
of the same age.
2. They will have difficulty agreeing on
which twin will be older.
3. For those who do agree, they won’t
agree on the reasons for it.
4. They will have different calculations
for the age difference.
Understandably it’s complicated and ends up something like the
Ehrenfest Paradox, where everyone agrees relativity should somehow
apply but are not sure how to do it. Still, let’s see what
can be done.
Usually to analyse situations involving both aspects of relativity we
need to separately determine the contributions from SR and GR then add
them together. At least that’s how it’s done when calculating
the GPS 38-microsecond-per-day time difference.
Calculating the contribution from SR should be easy because we know the
velocity at all stages. Presumably we would plug it into the
Lorentz transform and predict the amount of time dilation rate at any
point along the way. That is, we can determine how much
slower time will be running aboard the moving rocket.
Except that we have an obvious problem in that the Earth is moving away
from the rocket at the exact same velocity. And so Earth
should also be running slower than the rocket and by the same rate.
At this stage of the argument, relativists would typically resort to a
number of fall-backs:
- Start discussing other aspects of SR
such as length contraction, simultaneity, and additive velocities.
- Claim that both are running slower
than each other, and/or that the calculated amounts of time dilation
refer only to perceived rates of slow down, not actual slow down.
- Claim that the brief turnarounds are
all that is needed to break symmetry and cause one twin to be several
months older than the other.
- Claim that the small amount of
acceleration at lift-off is all that is needed to break symmetry and
cause one twin to be several months older than the other.
- Ignore the thought experiment and
discuss various real-world experiments.
- Claim that only the rocket slows down
because the Earth is somehow a special/universal reference frame that
all velocities need to be compared to.
- Claim that SR only applies to the
rocket because it experiences acceleration.
These are popular claims, and it’s worth addressing each of them before
covering the final point (7) in detail:
1. Start discussing other aspects of SR
such as length contraction, simultaneity, and additive velocities.
This isn’t going to help because the situation is
symmetrical. Whatever you apply to one clock you must also
apply to the other, affecting both clocks by the same degree.
So the situation remains symmetrical and there is still no way of
selecting one clock over the other.
2. Claim that both are running slower
than each other, and/or that the calculated amounts of time dilation
refer only to perceived rates of slow down, not actual slow down
This claim is nullified because the story involves the clocks coming
back together and compared side-by-side. If time dilation was
only perceived/illusionary on the first quarter of the journey, then it
would have to be perceived/illusionary on all quarters since they all
involve the same amount of acceleration. This is particularly
true of the transition from the second to third stage because
acceleration stayed perfectly constant during that time.
3. Claim that the brief turnarounds are
all that is needed to break symmetry and cause one twin to be several
months older than the other.
Note that the turnarounds represent at most 100 seconds out of 40
months and the challenge question asked you to ignore any time
differences arising from these moments. For someone to claim
this could cause one twin being several months older than the other
must be desperate. Astronauts experience strong accelerations
and long periods of weightlessness without becoming noticeably
younger. Aside from that, the person claiming this is also
saying none of these months of difference would have accumulated prior
to the first turnaround.
4. Claim that the small amount of
acceleration at lift-off is all that is needed to break symmetry and
cause one twin to be several months older than the other.
This is another desperate claim. The rocket lifts off at very
slow constant velocity, e.g. at a snail’s pace. Now it is
true that to get this initial velocity requires a small amount of
acceleration. And perhaps that tiny amount somehow shifts the
rocket into a different ‘reference frame’ that allows a time difference
to steadily accumulate. Fortunately this can also be overcome
by modifying the experiment to say that after lift-off, the rocket will
delay applying its own acceleration to make up the
difference. That is, the rocket clock will experience a brief
period of <1G to compensate for the brief period of >1G.
5. Ignore the thought experiment and
discuss various real-world experiments.
This is a popular debating technique that allows opponents to avoid the
question. While such experiments are interesting, they can’t
be used to answer it because any number of explanations can be proposed
to fit the observations. Also, we can’t be sure if specific
experiments were properly conducted, making them uncertain.
Since this a thought experiment, all the information required to answer
it should be contained in the SR and GR theory – there is no need to
refer to actual experiments. Respondents need to explain how
the theory answers the question. If it can’t be answered by
the theory then the theory is deficient.
6. Claim that only the rocket slows down
because the Earth is somehow a special/universal reference frame that
all velocities need to be compared to.
Relativists never say this outright but they often end up stating it
indirectly. Seeing that the Earth is now located in
intergalactic space, this is going to be very difficult to justify, if
it were not difficult enough already. We have known since the
time of Galileo that the Earth has no special position in
space. And in fact Galilean Relativity is contained in the
first postulate of SR. So SR followers have no excuse to be
ignorant of it!
7. Claim that SR only applies to the
rocket because it experiences acceleration.
This is often what gets brought up when discussing the traditional
Twins Paradox story. But seeing as the Earth twin experiences
the same amount of ‘acceleration’ as the rocket, this would also appear
to be an invalid objection in this case.
The Principle of Equivalence
This brings us to the focal point of the story. Namely that
the gravity/acceleration was the same for both clocks/twins, and
therefore according the to the Equivalence Principle, there should be
no way of selecting one clock over the other.
This principle can be stated a number of ways. Hyperphysics
does it like so:
“Experiments performed in a uniformly accelerating reference frame with
acceleration a are indistinguishable from the same experiments
performed in a non-accelerating reference frame which is situated in a
gravitational field where the acceleration of gravity = g = -a =
intensity of gravity field.” [1]
Einstein used a number of similar statements before settling on:
“Whenever an observer detects the local presence of a force that acts
on all objects in direct proportion to the inertial mass of each
object, that observer is in an accelerated frame of reference.”
Normally such experiments would involve dropping objects and watching
them accelerate ‘downward’ at a fixed rate independent of the object’s
mass. They could also involve watching a horizontal light
beam curve toward the floor (which will certainly happen if the floor
is accelerating upward, but is also said to happen in the presence of
gravity).
The experiment performed in this story involved atomic clocks and
finding how much faster/slower they ran in gravitational versus
accelerated situations. There is no falling involved but
nonetheless this is still an experiment by
definition. So presumably a clock in constant 1G
gravity should run at the same rate as a clock in constant 1G
acceleration. The fact that the clocks cannot be compared
while the experiment is in progress should not be an issue because when
the comparison eventually takes place, both clocks will have been
experiencing 1G at all times, other than the brief moments of
turn-around and lift-off/landing (whose microscopic contributions we
allow for in the comparison – we are looking for large time differences
in the order of months).
Time dilation due to gravity
Let’s now look at GR theory and see what it says about gravity, in
terms of predicting time dilation. Since time dilation is
often attributed to gravity, one might assume there must be an equation
that can tell you how much dilation will be caused by a given amount of
gravity. But that’s not the case. GR describes time
dilation not according to gravitational acceleration but gravitational
potential. These two things are very different.
Here is what the equation looks like [2]:
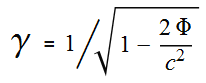 ---- (1) ---- (1)
Where γ (gamma) is the rate of dilation (the rate time slows down)
and Φ (phi) is the potential.
Gravitational potential refers to the amount of energy required to lift
a unit mass (i.e. 1kg in SI units) from its present height, all the way
to an infinite height.
We know that gravitational acceleration can be measured by dropping an
object and observing how it falls. We can also measure it in
terms of a static force, e.g. by placing a unit mass on some scales.
But gravitational potential is impossible to detect, let alone
measure. The only way to determine it is to measure the
acceleration function of gravity all the way to a height of infinity,
which obviously can’t be done.
In theory you could also determine it by multiplying the surface
gravity by the radius of the planet you are on. But this
would only work if the planet was: (a) spherical, (b) non-rotating, (c)
of uniform density, or the density was ‘radially symmetric’ i.e.
identical at any given radius.
So how is it possible for clocks to time-dilate according to something
that can never be detected? Not just detect from where they
are located, but not detect no matter how they move about, assuming
they were allowed to.
Or are GR proponents saying that clocks are somehow aware of the shape
of the planet they are on, their density distribution, and their
distance from the mid-point? Do clocks have ‘remote viewing’
abilities? If so you’d think some relativity expert would
have bought that exciting fact to our attention!
Either of these claims should be seen as impossible. And this
alone is sufficient to demolish the GR gravitational time dilation
equation as a possibility. It also demolishes the Equivalence
Principle because it admits the time dilation ‘equivalence’ is not due
to acceleration but potential.
At this stage, there doesn’t seem much point in going further because
all the claims relating to SR and GR have been shown as
unworkable. Unless that is, you are a geocentrist and believe
clocks have psychic powers.
Still, there is another aspect that should be addressed: acceleration.
Time dilation due to acceleration
A final aspect to consider is the amount of time dilation due to
acceleration.
Relativity supporters often talk about how acceleration affects time
dilation. This is especially so when discussing the Twins
Paradox, because it allows them to describe non-symmetry and point to
that as the reason for one twin aging faster than the other (and
without having to explain why).
Therefore it will probably come as a surprise to learn that there is no
equation that allows you to determine time dilation in terms of
acceleration.
The reason you can’t make such an equation is that you first need to
‘neutralize’ the acceleration term and make it dimensionless.
To make such an equation for velocity is easy. Velocity has
the units ‘L/T’, which is ‘length divided by time’. So divide
that by c (the speed of light), which has the same units, and you are
left with a dimensionless quantity: v/c.
This quantity can then be manipulated in certain ways. In the
case of the Lorentz Transform, the quantity is squared, subtracted from
one, then square-rooted and inverted. This gives the familiar:
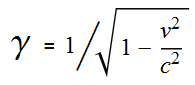 ---- (2) ---- (2)
But doing this with acceleration is a problem. Acceleration (a)
has the units L/T2. (length divided by
time-squared). You can multiply and divide that by c all you
like and it will never become dimensionless.
One way around it is to introduce a length (L) or time (T) into the
equation. E.g.:
a*L/c2
or
a*T/c
Both the above are dimensionless. But what length and what
time do we plug in? There are no special universal constants
available (other than Plank Units but they are too small).
This is also the reason why time dilation for gravity is in terms of
potential rather than acceleration. By multiplying
acceleration by a planet’s radius (a length), we get an expression
for potential which has the units L2/T2. And this can be
divided by c2 to ‘neutralize’ the units as shown in equation (1).
The closest SR comes to doing that when calculating time dilation due
to acceleration in a centrifuge. In this case they can
multiply the acceleration by the radius of the centrifuge, divide by
c2, and then insert it into something similar to gravitational time
dilation equation. Other than convenience, there is
really no justification for using the centrifuge’s radius.
But for linear acceleration there is no convenient distance to refer
to. At least not one that makes logical sense to include in a
time dilation equation.
In response to this, some might object and say that we do indeed have
such an equation for acceleration. It is of the form:
![T=\frac{c}{a}\text{ArcSinh}\left[\frac{a t}{c}\right]](img/RelCh2-eqn3.gif) ---- (3) ---- (3)
Two important points about this. First, it’s not an
expression for a rate of time dilation but for an overall time
difference. Second, it’s not in terms of acceleration but
velocity.
What this is is an expression for total elapsed time T experienced by a
clock that starts at velocity zero, and accelerates at a constant rate
of a for a duration of t. The full derivation can be seen on
Wiki [3]
What is happening is that the acceleration is being used to calculate
velocity at a particular point, which is being plugged into the regular
Lorentz transform. This gives a rate of time dilation
expressed in terms of acceleration and elapsed time, although it is
really based on velocity.
Except the aim of the exercise is to determine the overall amount of
time dilation. So it integrates this rate of time dilation
over a duration from 0 to t, giving the final equation (3) as a total
elapsed time experienced by the moving object.
By not including v into the equation it looks like the equation is
based on acceleration, when in reality it is entirely based on v, and
a and t are just shown in place of v.
In essence, this equation doesn’t justify why the experience of
acceleration should cause one clock to run slower than
another. It just allows us to calculate their relative
velocity. As such the equation should be applied equally to
both clocks.
Very deceptive. But then, what else would you expect from
relativists?
Acknowledgments:
Credit goes to Tom Hollings for the original story idea.
Tom’s website discussing various problems with Relativity is here:
http://problemswithrelativity.com
The original scenario was first put on this forum:
https://boards.straightdope.com/t/my-problems-with-relativity/388750/125
It’s worth reading the various excuses from the relativity supporters
as they try to ‘solve’ it. Their creativity is amazing!
[1]
http://hyperphysics.phy-astr.gsu.edu/hbase/relativ/grel.html
[2]
http://hyperphysics.phy-astr.gsu.edu/hbase/relativ/gratim.html
Although most references use G*M/R in place of Φ (potential), or they
use g*R. When calculating the time dilation at the centre of a
planet, you need to use Φ = (3/2)G*M/R
[3]
https://en.wikipedia.org/wiki/Time_dilation#Hyperbolic_motion
|

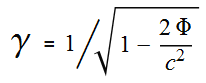 ---- (1)
---- (1)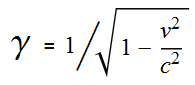 ---- (2)
---- (2)![T=\frac{c}{a}\text{ArcSinh}\left[\frac{a t}{c}\right]](img/RelCh2-eqn3.gif) ---- (3)
---- (3)