Cosmology – part 2

The Gunslinger and his Motorbike

An interesting analogy can be made about the interactions between charged particles. It runs as follows...

A man sits atop a stationary motorcycle, pistol in hand, arm outstretched and aiming forward. He fires a shot. Revving up his bike, he then accelerates in pursuit of the bullet. After achieving a certain velocity, he again takes aim along the same trajectory and fires a second shot. What will happen?

Assume that both bullets are neither affected by gravity nor air resistance. This allows them to move in perfectly horizontal lines at constant velocities. The first bullet has a good head start. But the second has the advantage of added initial velocity. At some point it will catch up and strike the first from behind.

Now let’s modify the bullets a bit. We’ll say they can somehow overlap and pass through each other. We’ll also say that when they overlap they form a combined bullet of the same size but double the mass. In this case the second bullet would merge into the first from behind and temporarily form a combined bullet. It would then pass out the front of the first bullet, leaving it trailing behind at lower velocity.

We’ll now add to the situation and say that as the motorcycle accelerates, the biker fires a steady stream of bullets, all on the same trajectory. Because of the steady acceleration, each bullet starts out with a higher initial velocity than the one before it. That means that each bullet will eventually catch up to and overtake the one before it. In fact, each bullet will ultimately pass through and overtake all bullets fired earlier on.

What the biker has could be described as ‘ghost bullets’ due to their ability to pass through each other. But let’s limit this ghostly property to interactions with other bullets and say that they strike other objects the way normal bullets would.

When one of these bullets strikes a target it exerts force. The force applied will be proportional to the bullet’s momentum, i.e. its mass times velocity. So far so good. Now here is where it gets interesting. When two bullets overlap they form a combined ‘super bullet’. This super bullet has double the mass and hence (assuming the same velocity for both bullets) double the momentum of a single bullet. So if it hits a target it will apply twice the force.

Getting back to the motorcyclist, you may be wondering why he is shooting in the first place. Well the reason is he’s a vandal and trying to punch a hole in a metal road sign up ahead. The sign is too thick to be punctured by a single bullet. And even if he stood firing one after the other at the same spot he’d make no progress.

But it happens this vandal is also a part-time physicist and knows it’s possible to overlap his special ghost-bullets for maximum effect. With the right timing, he knows it should be possible to fire ten in a row and get them all to overlap at the same point. If they overlap at the point when they hit the sign, they’ll hit it with ten times the force of a single bullet and punch a hole straight through.

The oddly accelerating particle

The story just told represents an analogy for what might occur on a much smaller scale with charged particles. Take an electron for example. We know it carries a charge and emits a constant electric field. In an earlier chapter this field was described as being analogous to a stream of tiny bullets. These ‘bullets’ radiate from all directions at light speed. When they strike another charged particle they impart a force.

We’ll start by assuming our electron is perfectly still and has been that way for some time. We now take that electron and move it slowly to the right. Referring back to our analogy, the electron is the gun and its field is a stream of bullets moving to the right (the field radiates in all directions of course but we’re only looking at the part moving right). As the electron moves right it continues to radiate ‘field bullets’ and these will move right with an added velocity, just like those fired by the biker after moving. Therefore, just like the biker’s, the electron’s later bullets will at some point catch up with its earlier ones.

The basic point here is that the field emitted by a moving electron must eventually catch up with a field emitted from the same electron when it was stationary earlier. It may take a long time and occur far away, but it must happen.

So what will happen when the later and earlier field overlap? Not a lot, other than there will be a temporary peak in the field strength at that point. This means that if there is a charged particle at that location it will feel (roughly) double the force. But other than that, not a lot.

Back to our biker vandal. His goal remember, was to punch a hole in a road sign up ahead. He knew that to do this he needed to overlap multiple bullets at once, and have them overlap at where they strike the sign. He estimated ten bullets should do the trick. His first attempt involved accelerating at a constant rate and firing at half-second intervals. It was a failure. The bullets ricocheted off the sign in an uncoordinated cacophony.

Examining high-speed footage from cameras placed along the roadside (yes he brought them along), he noticed the bullets passed through and overlapped each other at different points along the way. Not good. They needed to overlap at the same point and where they hit the sign. Realising that a fixed rate of acceleration was not going to do the trick, he set to work figuring out what will. Eventually he came up with a function describing an acceleration that increases as he approaches the target. Switching his high-tech bike to auto pilot, and entering the acceleration function into its on-board computer (nice bike!), he set off in direction of the sign, firing a volley of shots.

Success! The bullets overlapped at the sign and punched right through.

Super-intense overlapping of fields

By now the analogy I’m working toward should be obvious. So I’ll go ahead and ask: What would happen if our electron accelerated like the biker above?

The electron ‘shoots’ a field rather than bullets. The speeds are faster and the distances shorter. Yet the same principles apply. The logical answer to this is that the accumulation of its field emissions will overlap at a single point as this diagram shows.

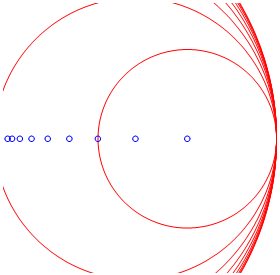
Here the electron starts motionless on the left and accelerates to the right. The blue dots show the electron at fixed intervals. The red circles are field pulses, one corresponding to each blue dot. The electron accelerates in such a manner that these field circles steadily merge. Then at one brief instant they all overlap and cause a large spike in the field strength. The pulses then diverge and the spike is gone.

In reality of course, the electron doesn’t emit pulses but a constant field stream. But the result is the same: a temporary spike in field strength [1]. If there was nothing at the point where that spike occurred (no charged particle) then nothing would occur. But what if there was, say, another electron there?

That second electron is akin to the road sign. In the case of the sign the multiple overlap of bullets punched through it. Could the large field spike cause similar damage to a target electron?

Probably not. The electron is light and not tied down. Most likely all that will happen is that it will receive an almighty kick that accelerates it to light speed in no time flat. So let’s change the situation a bit. Say the target electron is sitting still while two ‘attack’ electrons accelerate toward it from left and right sides, as shown:

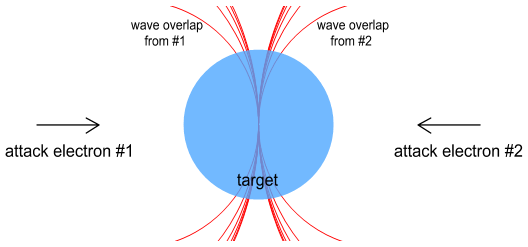
Both attack electrons mirror each other’s motion, i.e. they have the same starting position and acceleration profile, just in reverse. The result is that two field-spikes will hit the centre electron from the left and right sides. So what effect might this have? Again, probably nothing much. Since the spikes are coming from different directions, their forces are opposite and should simply cancel.

But let’s change the situation slightly and say that the spikes hit the electron on opposite sides as shown:

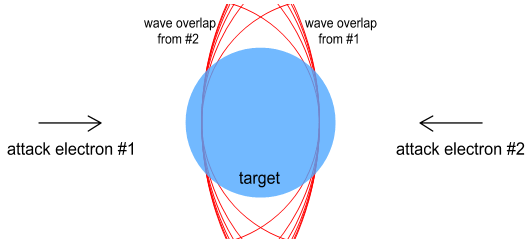
In this diagram the spike from the left-approaching attack electron hits the right-hand side of the target electron, and the spike from the right-approaching attack electron hits the left side of the target.

The situation now is quite different. The middle electron feels two opposing forces. Its left and right sides are being pulled in opposite directions.

In the chapter on subatomic particles we looked at the internals of charged particles and there I suggested that a charged particle consisted of a mass-core surrounded by a layer of charge, made of ‘charge substance’. I also pointed out that the charge within a particle must be constantly repelling itself, e.g. that the left and right hand sides of an electron would push against each other, causing the electron to fly apart. I then suggested that the mass-core within a particle provides a binding force that holds the charge together.

Whether or not you accept this theory is unimportant. The point is, if you agree that charged particles have a finite size then you would have to agree that the charge within them must be in constant repulsion against itself. And therefore, there must be some counter force holding this charge together. This force must be quite strong because it is able to confine the charge within a small volume. But... it cannot be infinitely strong.

Other than the limits of space and time, we know of no infinites in nature. No infinite masses, velocities, charges, energies, and certainly no infinite forces exist. Put another way, all physical quantities that can be confined within a limited range of space or time are observed to be finite. Therefore it seems reasonable to say that this force holding the charge together, whatever it is, must also be finite.

So here we have our hapless target electron stuck in the middle of two ‘attack’ electrons. It has just received a force on both sides, pulling the sides away from each other. The spikes that delivered that force are thousands, possibly millions, of times stronger than the force between two adjacent electrons. Therefore, it seems reasonable to say that at some point the force from these spikes will overpower whatever it is that’s holding the charge together. As the saying goes: ‘something’s gotta give’.

At this point the target electron should be torn apart and its charge scattered in opposite directions. Then what? Obviously we don’t know as we’ve never observed anything like this. So here the discussion becomes rather more speculative than before.

The Big Erasure

With no longer any binding force holding it together, the charge substance that was previously attached to the target electron scatters outward. How would it scatter? In the chapter on faster than light travel I described a situation in which a collection of like-charged particles bunched close together and released could accelerate to many times light-speed. This is effectively what we have here. The charge-substance that made up the electron is now free to move. It will accelerate to many times light speed. Now it might be supposed that the acceleration will be infinite because charge substance has no mass. But this will not be the case because the substance will encounter weak electric fields from other particles and from itself, and this will act to retard the acceleration slightly.

The charge spreads outward, reaching thousands of times light speed. As it does so, it continues to radiate electric field. When this field hits another charged particle, it does so at enormous speed and therefore exerts enormous force. Just like the original target electron, that charged particle is then shattered; its charge substance likewise scattered and accelerated to immense speeds.

This process continues in an exponential cascading effect. More particles break and expand, their ejecta breaking ever more particles. Within a short time every particle in the entire universe is destroyed and its charged scattered.

The space which used to occupy the physical universe is now filled with charge-substance. In addition to this, the mass-substance that originally held this charge together is also scattered because it no longer has surrounding charge to hold it together. So now what? Does the charge substance continue expanding? Well, perhaps not, because the universe is now filled with charge-substance of both types: positive and negative. And these two substances attract each other. Not only that, the mass substance attracts both of them.

What we have now is a sort of ‘primordial soup’, made of scattered mass and charge substance.

Being attractive, at this point the ‘soup’ begins to collapse in on itself. Like a deflating balloon, it shrinks down into smaller and smaller volumes. At some point the density of this soup increases to the point where concentrations of mass-substance can condense into mass cores with enough strength to attract quantum units of charge around them and form new subatomic particles (see subatomic particles).

The particles initially form at random and different sized cores lead to charged particles of differing mass. At this point, for some unexplained reason, the particles begin to duplicate themselves. Once one particle forms, it causes an identical one to form, leading to huge numbers of similar particles. The reason for this duplication process is unknown – but of course, this is a speculation designed to fit the observation that our universe contains only a limited number of particle types.

Having formed, the particles then start arranging themselves according to natural patterns such as nucleons and atoms. The formation of particles into various groupings causes them to be rapidly scattered in numerous directions. At this point a new universe is born.

A new kind of Big Bang

What I’ve just described sounds somewhat similar to the big bang theory. And in part it is. However there are some important distinctions. First, the explosion had a prior cause, it didn’t just occur spontaneously and for no reason. Second, the explosion was an expansion of matter, not an expansion of space. Third, the event is repeatable. [2]

So the basic story is this: Our current universe is one in a long line of universes, each of which self-destructed and reformed. The triggering mechanism for destruction was due to the movement of charges moving in opposite directions with a specific acceleration profile. This would come about naturally due to the random movement of particles throughout the universe. Getting the exact acceleration profile is an extremely rare event and possibly happens only once in a trillion years. But once it does happen and two such accelerating particles line up with an appropriate target particle, that particle explodes and the rest is history.

This is what a timeline of universe formation might look like:

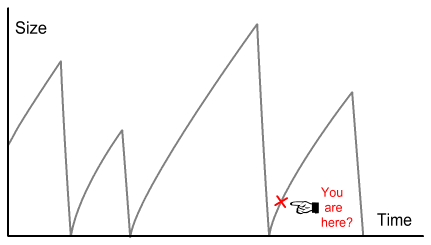
The vertical axis is the size of the universe and the horizontal one is time. As can be seen, each prior universe grew slowly and collapsed suddenly and then a new one formed. Note that each universe had a different lifespan, depending on when the catastrophic ending event occurred. Our current universe might be 100 billion years old (13.7 seems too short for extensive galaxy formation). Its end date is not known but could be 10 times that.

Where did all the anti-matter go?

One of science’s perplexing mysteries is the large imbalance between matter and antimatter. For example there are huge numbers of electrons, but almost no positrons. And there are huge numbers of protons but almost no anti-protons. As far as we know, the only difference between matter and anti-matter is the sign on their charge. Everything else is the same. If you could replace all matter particles in the universe with their antimatter equivalents, and vice versa, everything could continue functioning normally. Therefore, given that they are equivalent, why should one type outnumber the other?

In an earlier chapter on particle physics I talked about how positrons and electrons could overlap to form neutral composite particles (called poseltrons). It might be tempting to think therefore that that accounts for the missing antimatter. Unfortunately it can’t because this process removes equal numbers of matter and antimatter particles from view.

Fortunately there may be a simpler explanation at hand. What if the universe does contain equal amounts of matter and antimatter substance but we don’t see both at once because they repel each other? In the chapter on gravity we looked at how the orbital motion of quarks inside protons and neutrons could cause additional attractive and repulsive forces that would not be predicted by applying Coulomb’s law alone. In there I showed that a proton combined with a single stationary electron would exert a net attraction on a negative charge and a net repulsion on a positive charge. That means a proton+electron combination would attract an electron but repel a positron.

I also showed that a proton+electron combination would repel an antiproton+positron combination. Based on these situations it appears that the most common forms of matter and antimatter will repel each other gravitationally.

So here’s the scenario. In the early stages of the universe, equal amounts of antimatter and matter were created. In fact, matter and antimatter particles possibly formed simultaneously, as positive/negative pairs. The matter formed itself into proton+electron combinations (hydrogen molecules) and the anti-matter formed into anti-hydrogen molecules. The matter and antimatter repelled each other gravitationally into different parts of the universe. The only antimatter left behind was a few grains that got bound in with the matter. We just happen to live in a region dominated by matter. The antimatter will be far away now. Entire galaxy clusters will be made of antiatoms: positrons orbiting nuclei made of antiprotons and antineutrons. These galaxies will also contain the odd electron here and there but mostly bound up as poseltrons. Perhaps we can also see these galaxies from earth but they look the same as galaxies made of regular matter.

Multiple universes?

Another mystery has to do with the size of the universe. As pointed out in Part 1, our universe is likely to be physically finite, but surrounded by an infinite sized space. This is all well and good but it does raise a somewhat metaphysical question. In Part 1 we also looked at probability, and there I pointed out that an event with non-zero probability must reoccur at some point. And given an infinite amount of time, the event must reoccur an infinite number of times. Based on this I concluded that if there was such a thing as a big-bang, then it should reoccur on a regular basis.

When we talk about probability we are usually talking in terms of time, as in: what is the likelihood of an event occurring during a given time interval? But we could also talk about probability in terms of space. For example: what is the likelihood of finding an object in a given region. In this case the question will be: what is the likelihood of finding our universe within a given region (volume) of space?

To answer this we need to divide the volume of the physical universe by all available space. The universe is extremely large but still finite. When you divide the finite volume of the universe by an infinite volume of space you get zero. What this tells us is that the probability of finding the universe within any randomly chosen region of space is zero. Now that’s a problem because it’s effectively saying that the universe doesn’t exist. If the universe is physically finite in size, then, in comparison to an infinitely sized surrounding space, its size is zero and essentially non-existent.

Except of course, the universe does exist. No doubt many would object that this is just playing mathematical word-games. Nonetheless it can’t be denied that the size of a finite universe, large though it is, is zero in comparison to the space surrounding it. And zero size is essentially non-existence.

Solving this conundrum does seem to require that there be more than one universe. In fact it requires that an infinite number of universes be spread throughout space. Why so? Well, since our universe exists in this region of space, that means it has a non-zero probability of being there. This means there is a non-zero probability of another universe existing elsewhere. Given enough space then, we can guarantee that another universe will be found in it. And given an infinite volume of space, we can guarantee an infinite number of universes.

These universes will be located very far from ours. They will be in different stages of growth. The particles they contain will have been randomly generated and self-duplicated at the start of each universes’ growth. Therefore they will be different from ours, in terms of mass, although each will have the same quantum of charge. Occasionally some of these particles will be accelerated to super light speeds, like those mentioned in the faster than light chapter. Since they are moving much faster than the light coming from that universe, it’s possible that these will cross over into other universes, such as ours. These particles may then account for some of the very rare particles found on earth.

In each of these universes the basic physical laws will be the same: they will each have the same speed of light and the same integer unit of charge.  But due to differing masses of common basic particles, other ‘physics laws’ will be different.  For example Plank’s constant and Newton’s gravitational constant will have different values.  In fact the phenomena of gravity may not be present at all, or at least not in a form familiar to us.  This is because atomic nuclei, which allow such a thing as gravity (see gravity), might not exist in all universes.  And without atomic nuclei the concept of Plank’s constant would also have no meaning.

Further interesting premises stem from this.  In some universes, such as ours, the subatomic particles will allow for the formation of complex molecular structures like carbon-based DNA and this will allow life to exist.  In other universes (probably most) the formation of complex molecular structures will not be possible, meaning that life forms will be unable to exist there.

Olbers’ again

This possibility of multiple universes leads us back to the earlier mystery of Olbers’ paradox. If there are infinitely many universes shouldn’t their light eventually reach us and fully illuminate the night sky?

Coulomb’s law tells us that the electric field generated by a charged particle extends to infinity. As it travels, this field spreads out spherically and becomes weaker – much like an expanding balloon whose skin becomes thinner. To reach unlimited distances requires this field become infinitely weak but without becoming zero. Is that possible?

When we look at a nearby star, the light we see comes from the activity of the electrons on its surface. That means the field from individual electrons has travelled several light years at least. The field strength from a single electron over that distance would be extremely small. For distant galaxies the strength becomes far smaller again.

To make matters worse, the field from a single electron comes from the charged region within it. This means that each tiny part within that region is generating a field that spreads over a sphere of billions of light-years radius, and without becoming zero.

Is it possible for the electric field from individual electrons, or from parts within them, to become thin without limit? In some ways this seems difficult to fathom because quantities like mass and charge seem to have non-zero limits. Yet the fact that we can see distant galaxies means the field their electrons generated did reach here.

Well perhaps there is a limit on how thin a field can get before ceasing to exist. And perhaps the reason we see distant galaxies is that the field from numerous emissions combines and this is allows it to cross large distances.

What I’m suggesting is that the field from a single electron can travel only a certain distance before becoming too thin and cutting out completely. Whereas the combined field from two electrons can travel double that distance. In this way we are able to receive light from distant galaxy clusters because the combined strength of many fields enables it to reach earth.

But in the case of other universes, the gap between them is too great due to all matter from the previous universe being removed during the ‘big erasure’. Thus their light becomes too thinly stretched and disappears before it can make it to a neighbouring universe.

-----------------
[1]  The acceleration needed produce a simultaneous overlap of fields from a charged particle is a = c²/(d-c t), where d is the initial distance from the target. This makes the velocity function v = c log[d/(d-c t)], and the distance function x = c t-(d-c t) log[d/(d-c t)]. The strength of the final overlapping pulse will depend on how far away the starting point is.
[2]  This idea is also similar to a theory called Quasi Steady-State Cosmology (QSSC) [by Hoyle, Burbidge and Narlikar, 1993], except it doesn’t require gravity for the collapse stage. http://casswww.ucsd.edu/personal/gburbidge.html