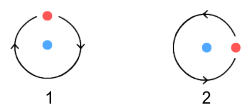Gravity

Gravity is described as an attractive force between masses. It is the oldest known and most well-observed of the known forces. Yet often considered the least understood.

As far back as 1676 Isaac Newton described gravity via an equation that stated its force was proportional to the product of two masses and inversely proportional to the distance between them. This much could he could confirm from the motion of planets and other astronomical bodies and the behaviour of objects on Earth. But what Newton could not be sure of was why gravity behaved as it did or why it occurred at all. He later wrote “I have not been able to discover the cause of those properties of gravity from phenomena, and I frame no hypotheses ...”.

Since that time, little else has been learned about the nature of gravity other than it appears to propagate at light speed, based on observations of mercury’s perihelion.

So what could be the mechanism behind gravity? Yes we understand it to be a force between masses, but how does mass ‘communicate’ such a force? Based on the inverse square relationship and its limited propagation speed it seems that gravity propagates as a field – much like an electric field, except generated by mass rather than charge and always attractive. It’s as if every subatomic particle radiates a field with strength proportional to its mass. That field then spreads spherically outward at light speed, weakening as it goes with inverse-square strength.

The fact that a gravity field moves at light speed raises some interesting questions. When that field strikes another mass it applies a force in the opposite direction. This sounds somewhat similar to the attractive force between oppositely charged particles. As explained throughout this book, such as with magnetism, there is ample reason to believe that electric forces are based, not only on charge and distance alone, but also velocities. Therefore one might wonder whether gravity might work in a similar way also. For example would gravity increase as an object moves away from another mass, like an electron moving away from a proton? And would gravity decrease as an object moved toward another, falling to zero as the incoming object approached light speed?

Electrical effects of Gravity?

Such questions are interesting. But rather than speculate on simple points like that, it would be more helpful to understand gravity on a more detailed level. Earlier on we saw how magnetism between two wires could be explained in terms of neutral charge movements. The two wires were electrically neutral yet were able to exert a net attraction or repulsion on each other. A similar phenomenon occurs with static electricity in which charged objects are able to attract neutral objects, even when such objects cannot be “polarised” according to the theory of how static electricity is said to operate. Therefore one might wonder if similar motion-based electrical effects might be responsible for gravity.

Of course there are great differences between gravity and magnetism. For one, the gravitational force is extremely weak and only becomes noticeable when dealing with large clumps of neutral matter, usually astronomical bodies. Secondly, gravity is always attractive and has no ‘poles’.

Those quarks again

In the preceding chapters we looked at atomic nuclei as being active arrangements of moving quarks. It that model, positive up-quarks orbited negative down-quarks and embedded electrons. This motion was sufficient to explain the strong nuclear force and possibly the quantum mechanical nature of electron orbits. Could it have any effect beyond these things? Let’s look at a proton again.

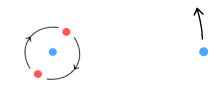
The above diagram shows the simplest of atoms – hydrogen. The situation is overall neutral with two up-quarks orbiting a down and an electron at a distance. The aim here is to determine the overall effect of this movement on similar atoms nearby. The situation is a bit complex and contains many particles so let’s simplify it a bit:

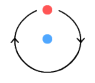
Here we have a single up-quark orbiting a stationary down-quark. Obviously this arrangement is not the same but since the up-quarks have the same motion we can study the effects from just one of them. As for the electron, it is moving relatively slowly compared to the quarks so we can treat it as being basically stationary like the down-quark. What we’ve effectively done is combine the up-quarks together and combine the electron into the down-quark. We’ll start by looking at what effect this will have on a positive charge.

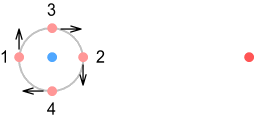
Above we see a positive charge sitting in the same orbit plane as the up-quark. We’ll look at the force from four points in the orbit: left, right, top and bottom and labelled 1,2,3,4 respectively. As the up-quark moves toward the positive charge (point 3) it exerts an increased force, and as it moves away (point 4), force decreases. As it moves up and down (points 1 and 2) its force decreases slightly. Doing the math shows the overall contribution from these points yields a net increase in repulsion. If we wish to know the contribution from all possible points in the orbit, this requires integrating around the circle. Doing this shows, as might be expected, that the overall force has increased and the orbiting up-quark pushes the positive charge away.

So if quarks orbiting within a proton can increase their push on a positive charge, what will they do to a negative one? If we replace that positive charge on the right with a stationary electron we can calculate the net contribution from all points around the orbit. Due to the increase in attraction from the positive charge moving away (point 4), it should come as no surprise that net contribution is negative and the electron will be attracted. This is similar to the net-attraction described in the static electricity chapter.

Let’s repeat the above with a bit of math. Consider the diagram below:

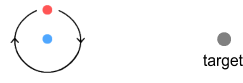
On the left is a positive up-quark closely orbiting a negative down-quark. On the right is a target particle sitting at a distance of one unit. The up-quark is orbiting in the same plane as the target. All charges have a unit charge of one, such that the force between two particles at a unit distance will be one force unit. We will also say the up-quark is moving at 10 percent of light-speed, i.e. 0.1c. Here are the results:

If the target particle is positive it will experience a force of +0.0325 (repulsive)
If the target particle is negative it will experience a force of -0.0024 (attractive)

These numbers come from integrating the force around a circle. It seems the attractive force on the negative target is rather weak by comparison. This is due to time-decay of the field strength as the positive up-quark (at point 4) moves away from the target.

Changing orientations

Okay, so we know what happens when the target particle lies in the same plane as the orbiting up-quark. What would happen if we turned that orbit plane around? See diagram:

Here the orbit plane is at right angles to the target particle. Here are the results:

If the target particle is positive it will experience a force of -0.0344 (attractive)
If the target particle is negative it will experience a force of -0.0247 (attractive)

This is a very interesting result. Both negative and positive targets are now being attracted. How did this happen? The reason is that the up-quark is always moving away from the target so its virtual-current particle will be located far from the target. This means it can’t repel the positive target very well and hence we are left with a net attraction toward the down-quark. But at the same time, the away-movement is sufficient to cause a net increase on the attraction of the negative target.

Attraction between two circular orbits

The above calculations show the net force exerted on a stationary target particle by an up-quark moving in different circular orbits. Let’s now extend that to look at the force between two such orbiting quarks. Start with this situation:

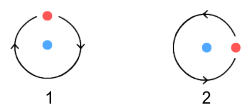
Here we see our two ‘protons’ with their up-quarks in the same orbit plane. The phase-angle of the quarks are random and not aligned between the two protons. We wish to know the net force on the proton on the right. The net force will be the sum of four force component quark combinations: up2 & up1; up2 & down1; down2 & up1; and down2 & down1 (where 1 and 2 respectively represent the left and right protons).

This gives a net force of +0.03015 (repulsive)

And the two protons repel each other. The above number was calculated from the average of all possible points on one orbit (of proton 1) to all possible points on the other orbit (of proton 2).

Now we’ll redo the above but this time with the orbit planes facing each other (again, the phase between up-quarks is unmatched):

This setup yields a net force of -0.05930 (attractive)

So this time the protons attract each other.

Going the full sphere

The above situations show how the net force between two protons can vary greatly, depending on orientation. What this tells us is that it’s possible for protons to reduce the amount of static repulsion that would be predicted by Coulomb’s law. This means that if we add electrons to neutralise the situation, i.e. by making atoms, there can be a net attraction between such atoms, provided that they are suitably aligned.

In reality however, we can’t assume protons to be aligned in specific orientations. Within a large clump of matter, protons will be randomly aligned in all manner of directions. Therefore to determine the net effect from all possible orientations it is necessary to repeat the above exercises but this time by integrating over the surface of a sphere. See below:

On the left is our up-quark orbiting the down-quark in random directions over the surface of a sphere, in which the pink sphere represents all possible positions of the red up-quark. On the right is a static target particle. We will consider the situations where the target is positive and negative.

If the target particle is positive it will experience a force of +0.010013 (repulsive)
If the target particle is negative it will experience a force of -0.009853 (attractive)

Just as with circular orbit on the same plane as the target, the ‘spherical’ orbit repels the positive charge and attracts the negative one. The difference here though is the magnitude of the forces is lower and they are closer together.

Now take this to the next step, which is to have two spheres. See diagram:

Here both the source and target consist of up-quarks orbiting a down-quark. The orbits are circular, however, since we must consider all possible random orientations, we treat them as ‘spherical’. Determining the net force in this situation requires integrating all possible positions over one sphere versus all possible positions over the other. It’s a four-way integration, and very complex. But here is the result:

The net force is + 0.0001369 (repulsive)

This is a bit of a disappointment. What it shows is that the average force between atoms orientated in random directions is repulsive, rather than attractive. The opposite of gravity. The force between them is 7300 times weaker than the force between two stationary up-quarks – which is nice because we are searching for a weak force that might pass for gravity. Except it’s in the wrong direction.

Cutting a cone

Rather than quit at this point it is useful to investigate what might have gone wrong or if anything has been overlooked. The net force we arrived at was a combination of many factors. It consists of the interaction between different charged particles moving in different directions. The greatest degree of repulsion occurs when the positive quarks move directly toward each other. Therefore it would be interesting to know how much of this ‘direct toward’ motion would need to be removed from the equation to bring the net force down to zero and into the negative (attractive) domain.

This can be done by removing a small portion of the ‘sphere’ along the direction of a line joining our two protons. Basically cutting out a cone-shaped region from each as shown:

And then saying the up-quarks are restricted to orbiting within the remaining region. [Note: this diagram shows a mid cross-section of the cones – the cones don’t cut across the entire sphere as drawn]

After some experimenting, it can be found that this angle can be as narrow as 5.47 degrees in total, i.e. a half angle of 2.735 degrees, for the repulsion to cease and the ‘protons’ to begin attracting. In this situation the protons will have a net attraction of -2.6x10^-7 force units.

The above is certainly interesting because it shows that only a narrow region of the up-quark motion is responsible for the net repulsion of our ‘protons’. Therefore it would seem that if we could limit the motion of the orbiting quarks such that they don’t run directly toward each other, a weak attractive force would result.

Such alignment might naturally occur within a small clump of protons because the up-quarks would avoid moving directly toward other up-quarks, where they experience the maximum degree of repulsion. Problem is though, a large group of protons, such as would exist within a planetary body or even a small rock, cannot align themselves to face each other because they are not arranged in a line and are surrounded by protons on all sides.

Synchronization is the key?

There may be an answer however. When calculating the above net forces the assumption was made that quark movement is random, in that the quark orbits are aligned in random directions and have no relationship with each other. Well the overall alignment may well be random from one proton to the next, but the precise movement of the orbits is another matter.

As an up-quark orbits, it will encounter a certain degrees of both attraction and repulsion. An attractive force will cause the quark to speed up and a repulsive force will cause it to slow down slightly. As shown above, the greatest amount of force will be the repulsion that occurs when two quarks head directly toward each other. This may cause an orbiting quark to adjust its orbit such that that force is minimized. Basically we would expect it to synchronize with the movement of the other photon and adjust its phase so as to reduce the overall force to a minimum.

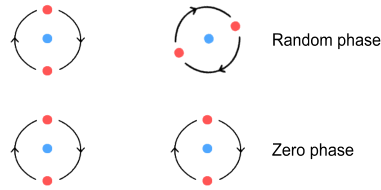
The above diagram shows an unsynchronized (random phase) situation versus a synchronized (zero phase) situation. Here the red up-quark has been split into two to represent the opposing quarks on the same proton and each up-quark is given a charge of +1/2 (the down-quark still has -1).

By experimenting with phase relationships we find the minimum force between two protons occurs when the opposing quarks have the same angle, i.e. the phase between them is zero.

To be specific, the force between the above situations is as follows:

Random alignment: +0.0301496 (repulsive)
Phase-lock alignment: +0.0300678 (repulsive)

We note here that the force is still repulsive but that is has decreased by an amount of 0.0000818.

Now let’s go back to our two-sphere model, in which the quarks between opposing protons move at random. In this situation they receive a repulsion of 0.0001369 units. Now let’s modify that slightly to say the quark orbits are overall random but when they sit in the same plane they synchronize with the same phase.

This would reduce the amount of force between them. To calculate the new force we subtract the above difference and get:

0.0001369 - 0.0000818 = +0.0000551

The force is still repulsive but has reduced substantially. To reduce it further we could argue that synchronization occurs over a narrow range when the orbit planes are almost lined up. If that were the case the net force could shift to negative and the protons (combined with stationary electrons) would attract. Providing this new level of attraction was low enough it could pass for the phenomenon we call gravity.

Cancelling the radiation

There is another reason to believe why the phase of two proton’s up-quarks should synchronize and why their phase should be zero.

The model of a single proton presented here has two positive up-quarks orbiting a negative down-quark. The up-quarks are exactly opposite each other and each emit a signal that precisely cancels the output of the other because it is 180 degrees out of phase.

Precisely? Not quite.

It’s true that if the up-quarks are directly opposite this will cause them to radiate signals that are 180 degrees out of phase, i.e. opposite, to each other. But the problem is they are not located in the same place. The up-quarks are located one-behind the other. This means there will be a short delay for the signal from the farther quark to reach the nearer one. The below diagram explains this:

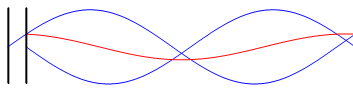
Here two electrons are moving in sinusoidal motion within parallel antennas, shown as black vertical lines. The voltage signals fed into each antenna are 180 degrees out of phase, i.e. they are mirror images of other. Now if the antennas were sitting right next to each other the two signals they generate (shown in blue) would completely cancel and we would detect nothing to the right of them. But since there is a distance between them they don’t completely cancel and we are left with a net signal as shown in red.

The amplitude of the combined wave will depend on the frequency and the time taken for the signal to pass between the two antennas. Shorter distances make for better cancellation and higher frequencies lead to less cancellation.

The proton is an analogous situation because the opposing up-quarks are one behind the other. This distance between them is very short and light travels very fast so the time taken for the signal to cross this gap will likewise be extremely short – but not zero. In addition to this the high frequency of orbit will reduce the amount of cancellation.

This means the up-quark signals will be slightly less than 180 degrees out of phase and will radiate a weak high-frequency field, probably in the high gamma-ray range. If this were the case we would certainly be aware of it. Except we don’t observe such radiation.

This indicates that the phase between protons has been matched. In order for a proton to adjust its phase it would either need to adjust its speed temporarily or reposition itself slightly toward or away from another proton so as to synchronize with its ‘up-quark waves’. In some cases the synchronization will be good, in other cases it will be partial. What matters however is only the overall average because that is what determines the net force between large clumps of matter. If that net force is both weak and attractive then it could pass for gravity.

Anti-gravity at a distance

There is a problem however with the above idea that synchronisation must occur between all orbiting quarks. Namely that it would be not be possible for synchronising to occur over unlimited distances. For example it would be very difficult for distant galaxies to synchronise with each other because their fields would be very weak.

But this problem may well be a blessing in disguise. If galaxies and galaxy clusters could synchronise they would exert a weak attraction on each other, and this would pull everything in the universe together. But being out of sync means, not only won’t they attract, they will instead weakly repel each other. It also means they will slowly accelerate away from each other.

There is a certain body of evidence to suggest that much of the universe is doing just that. Namely the phenomenon of redshift which occurs when light-emitting objects move away from each other [1]. To explain this physicists came up with the concept of ‘dark energy’ which is said to be a substance that makes up 75% of the universe and pushes it apart. With the concept of unsynchronised gravity however, it becomes unnecessary to invent such substances; ordinary matter can do the job on its own.

No Light-bending or Singularities

If the idea that gravity is the result of an interaction between electrical charges (rather than masses) is true, it has a number of important implications. Firstly it means that gravity won’t bend light. We know that laser beams and radio waves pass though each other without deflection. Therefore a light beam should not be disturbed by the electrical fields of gravity either. This means that any such observed bending is more likely the result of refraction as described in general relativity experiments.

A second point has to do with the concept of black holes. In the general relativity chapter I argued that the time dilation aspects of such bodies should not occur. And here I argue that they should not attract light either. But even if super-massive bodies neither attract light nor distort time, there is another aspect attributed to black holes that warrants discussion: the ‘singularity’. This is the idea that a massive object can collapse under its own gravity and into a point.

If gravity operated purely as a force between masses then we could arguably grow a force without limit. For example, imagine that we had access to a (very-very-very) large supply of sand and the ability to transport it to the planet Mars. We begin this experiment by steadily adding sand to its surface in an even manner. As time passes Mars grows ever larger and its surface gravity ever stronger. While this is happening the pressure at the core of the planet becomes steadily greater. The atoms at the planet’s core are being held apart by chemical forces, i.e. by repulsion between their orbiting electrons. This force is very strong but not infinitely so. At some point, e.g. when Mars becomes ten thousand times its original diameter, this force will become overwhelmed by the pressure of gravity.

At this point, speculatively speaking, the atoms might collapse into their nuclei, making the planet a ‘neutron star’. This collapsed planet would possibly be a thousand times smaller than its pre-collapse size giving it even higher surface gravity and higher internal core pressure. But we don’t stop there – we continue adding sand to its exterior. At some point the internal pressure will become so great that even those nuclei cannot withstand the force. At this point the structure would further collapse, its gravity increasing as it shrinks, and ultimately into a single point with infinite surface gravity: a ‘singularity’.

Such an outcome seems impossible because we now have a finite amount of mass contained in a zero volume. Yet this is precisely what gravitational laws predict. Seeing that common-sense physics principles do not allow for division by zero it would therefore be wise to consider a more-likely outcome of this sand experiment.

So here is another possibility. As the nucleons begin to collapse the quark orbital structures come apart. Since the orbital motion of quarks is what causes gravity, at this point gravity ceases to exist. Instead the entire structure blows itself apart… a supernova perhaps? In reality this explosion would probably occur at the earlier point where the nucleons come into contact with each other since it seems unlikely that quarks could orbit under such conditions. This would also mean a ‘neutron star’ is not a valid state for matter either.

Reversing the charges

Before concluding it is interesting to note what happens if we were to totally reverse the charges on one of the protons. That is, make the down-quark positive and the up-quark negative as shown below:

Integrating over two full spheres, we can calculate the net force between them to be +0.0004595 (repulsive)

That’s an interesting result because one might suppose that the moving positive quark on one proton would produce a strong attraction on the moving negative quark on the other. Instead, not only do they repel, the repulsion is 3.4 times greater than between identical protons.

Now it is possible to make them attract by ‘cutting a cone’ as per the above method. But to do this requires the cone angle to be around 10 degrees (a half angle of 5 degrees), which is nearly twice what was required for the two identical protons.

Hence it does appear unlikely that such opposite protons will be able to attract. The significance of this will become apparent in the second chapter on Cosmology.

Conclusion

It’s possible that the phenomenon we know of as gravity may be due to the interaction between of moving subatomic particles within nucleons. Particularly the rapid orbit of up-quarks and the relatively slower down-quarks and electrons.

This does not rule out the possibility that mass also generates a gravitational field that produces attractive forces on other masses. However any such force would be in addition to the forces that would arise from movement of electric forces described here. Therefore it may be that gravity is a combination from both force types.

The arguments presented in this chapter are largely descriptive and hence incomplete from a mathematical view-point. A proper proof that gravity is entirely result of electric forces will require deriving the gravitational constant G from first principles. Doing so will require knowing precise information about the size and charge-distribution of quarks (both types) and even electrons. It will also require huge amounts of numerical computation and simulation.

An exercise for another day!