Magnetism – Proof of Concept,
part 2

The preceding chapter showed that the Velocity Dependant Coulombs Law (VDCL) could be used to determine the exact result as Maxwell’s magnetic force equations. The example used however was simplified because it had the same current and cross-sectional area in each wire. Will the equations hold true in other situations? Here we’ll derive a general equation involving different currents and cross-sectional areas.

Consider the two wires in the below diagram:

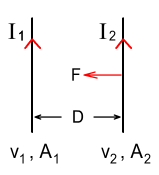
Wire 1 (at left) has a current of I₁ and a cross-sectional area A₁. Wire 2 has a current of I₂ and a cross-sectional area A₂. What will be the force experienced by wire 2?

We are dealing with more variables now so the maths becomes more complex. Fortunately most of the work has already been done in the preceding chapter and it’s mostly a matter of substituting new values into the old equations.

Let the velocity of the electrons in wires 1 and 2 be v₁ and v₂ respectively. Since the electrons are moving at different velocities we now also need to determine the force between them. Previously this was unnecessary because they were motionless relative to each other.

So there are four forces to consider:
F_ee = force from the electrons in wire 1 on the electrons in wire 2 (repels)
F_ep = force from the electrons in wire 1 on the protons in wire 2 (attracts)
F_pe = force from the protons in wire 1 on the electrons in wire 2 (attracts)
F_pp = force from the protons in wire 1 on the protons in wire 2 (repels)

We’ll start with F_ep. As before, we determine the force on the protons in wire 2 from the electrons at +x and -x (in wire 1). Taking the previous equations for F_p1 and F_p2; and replacing F_p1 with F_ep1, F_p2 with F_ep1, and v with v₁ we get:

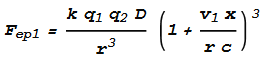
$\text{\textit{$F_{\text{ep1}}=\frac{k q_1 q_2 D}{r^3}\left(1+\frac{v_1 x}{r c}\right){}^3$}}$

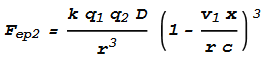
$\text{\textit{$F_{\text{ep2}}=\frac{k q_1 q_2 D}{r^3}\left(1-\frac{v_1 x}{r c}\right){}^3$}}$

Next we determine the force from the protons on the electrons, F_pe. This will be same formula as F_ep but with v₁ replaced with v₂:

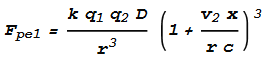
$\text{\textit{$F_{\text{pe1}}=\frac{k q_1 q_2 D}{r^3}\left(1+\frac{v_2 x}{r c}\right){}^3$}}$

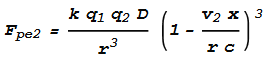
$\text{\textit{$F_{\text{pe2}}=\frac{k q_1 q_2 D}{r^3}\left(1-\frac{v_2 x}{r c}\right){}^3$}}$

Next to determine the forces between opposing electrons, F_ee. Let the force from the electrons at +x and -x be F_ee1 and F_ee2 respectively. Taking the above equations for F_ep, changing the force direction to negative, and replacing v₁ with -(v₁ - v₂) (the negative difference in velocity) we get:

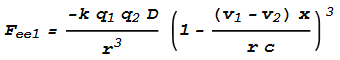
$\text{\textit{$F_{\text{ee1}}=\frac{-k q_1 q_2 D}{r^3}\left(1-\frac{\left(v_1-v_2\right) x}{r c}\right){}^3$}}$

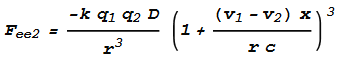
$\text{\textit{$F_{\text{ee1}}=\frac{-k q_1 q_2 D}{r^3}\left(1-\frac{\left(v_1+v_2\right) x}{r c}\right){}^3$}}$

Finally the force between protons, F_pp. This can be determined from F_ep1 + F_ep2 by setting v₁ to zero and changing force direction to negative. It is simply:

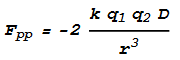
$\text{\textit{$F_{\text{pp}}=-2\frac{k q_1 q_2 D}{r^3}$}}$

The total force dF can be obtained by adding these seven forces together:

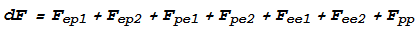
$\textit{dF}=F_{\text{ep1}}+F_{\text{ep2}}+F_{\text{pe1}}+F_{\text{pe2}}+F_{\text{ee1}}+F_{\text{ee2}}+F_{\text{pp}}$

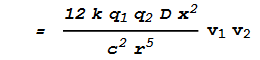
$\text{\textit{$=$}}\text{\textit{$\frac{12 k q_1 q_2D x^2}{c^2 r^5}$}}v_1 v_2$

Compare this with the corresponding formula in the previous chapter. Notice that the only differences are that the result has increased by a factor of 2 (12 instead of 6) and v² has been replaced with v₁ v₂.

The factor of 2 is due to looking at the force on the electrons in wire 2 from the protons wire 1 (F_pe), as well as the force on the protons in wire 2 from the electrons in wire 1 (F_ep). Whereas before we only looked at the force on the electrons in wire 2 from the protons in wire 1 (F_e). In other words we have double counted. To make this consistent with the previous chapter, we’ll reduce dF by a factor of 2:

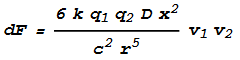
$\text{\textit{$\text{dF}=\frac{6 k q_1 q_2D x^2}{c^2 r^5}v_1 v_2$}}$

Next we need to express the velocities in terms of current, charge density and area. This yields:

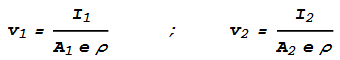
$v_1 = \frac{I_1}{A_1 e \rho }\text{ ; }v_2 = \frac{I_2}{A_2 e \rho }$

To continue from the calculations in the previous chapter, q₁ and q₂ will become:

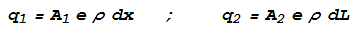
$q_1 = A_1 e \rho \text{dx}\text{ ; }q_2 = A_2 e \rho \text{dL}$

Substituting this in gives:

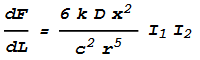
$\textit{$\frac{\text{dF}}{\text{dL}}=\frac{6k D x^2 }{c^2 r^5}I_1 I_2$}$

Compare this with the corresponding formula in the previous chapter. Notice the only difference is that I² has been replaced with I₁ I₂. Since this expression is a constant, we can skip the integration and substitute this expression into the final result. This gives:

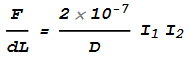
$\textit{$\frac{F}{\text{dL}}=\frac{2 10^{-7}}{D}I_1 I_2$}$

Substituting the ‘permeability constant’ μ₀ = 4*pi*10^-7, the above can be written as:

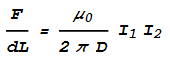
$\textit{$\frac{F}{\text{dL}}=\frac{\mu _0}{2\pi D}I_1 I_2$}$

Which is identical to the conventional magnetic force equation.

Conclusion

The Velocity Dependant Coulombs Law proposed here is able to match the conventional magnetic force equations in a general situation involving two wires carrying different currents, and this further indicates that the VDCL could be an accurate description of why magnetism occurs.

An added benefit is that we can use this method to determine the magnetic force in different situations. For example, we can use it to determine magnetic force between two wires of finite length. Because the conventional equation requires the ‘source wire’ to be infinitely long (while the ‘target wire’ can be any length), and this could never represent a real situation.

Magnetism – Proof of Concept, part 2

Conclusion

Magnetism – Proof of Concept,
part 2