GPS Mythology – part 2
Secondary relativistic effects
The preceding chapter examined claims regarding the necessary
application of Relativity to the Global Positioning System.
It argued that, providing the satellites orbited at the same altitude
and no adjustments were made to take Relativity into account, the
largest error that could accumulate over a 24 hour period would be an
unnoticeable 15cm.
This is nowhere near the enormous 11km that is frequently
claimed. Take this quote from Relativity promoter Clifford
Will for example:
“But at 38 microseconds per day, the relativistic offset in the rates
of the satellite clocks is so large that, if left uncompensated, it
would cause navigational errors that accumulate faster than 10 km per
day! GPS accounts for relativity by electronically adjusting the rates
of the satellite clocks, and by building mathematical corrections into
the computer chips which solve for the user's location. Without the
proper application of relativity, GPS would fail in its navigational
functions within about 2 minutes.” [1]
Is he kidding? Nothing much is going to accumulate over a two
minute period other than a miniscule error of 0.2mm. The only
thing this paragraph demonstrates is that the majority of Relativity
followers can’t think straight and function by blindly repeating the
words of other followers.
Another problem we have is that the stated 38μs-per-day adjustments are
made in the satellites rather than the receivers. The
satellites are military equipment and contain special encryption used
for accurate missile targeting. Hence a close examination of
them would be off-limits to almost everyone including the majority of
scientists. This makes the system somewhat inadequate as a
test for Relativity. Even those who work at the GPS
ground-monitoring stations with super-accurate clocks would be unable
to determine what adjustments are made: Perhaps the
satellites experience the stated amount of time dilation and
adjustments. Or perhaps they experience different amounts of
dilation and adjustments. Or perhaps they experience no
dilation and no adjustments are made.
All that aside, some might argue that GPS can still be a good test of
Relativity because there are a number of adjustments for ‘secondary
relativistic effects’ built into the receivers that we can verify
directly. The first has to do with imperfect orbits and the
second with the Sagnac Effect. The purpose of this chapter
will be to examine them, starting with the former.
Adjustments for eccentric orbits
In an ideal world, GPS satellites would be launched so as to sit in
perfectly circular orbits at predetermined altitudes. In this
way the amount of relativistic effect would be the same for every
satellite and have a constant value throughout its orbit.
Hence an identical timing adjustment could be programmed into each
satellite to negate the effects. Such an adjustment would
allow a GPS receiver not have to take relativity into account.
In the real world however, things don’t always proceed as
planned. The satellites instead end up with slightly
elliptical orbits. Because of this, the amount of time
dilation will vary throughout an orbit as the satellites experience
variations in their speeds and altitudes. And because of
this, the fixed amount of relativistic adjustment that is built into
satellites pre-launch is insufficient to negate the full effects of
relativity. Instead, the receiver needs to make some of its
own adjustments to get proper accuracy.
This May 2002 Physics Today article by Neil Ashby describes the
situation:
“If a clock's orbit is not perfectly circular, gravitational and
motional frequency shifts combine to give rise to the so-called
eccentricity effect, a periodic shift of the clock’s rate with a period
of almost 12 hours and an amplitude proportional to the orbit’s
eccentricity. For an eccentricity as small as 1%, these effects
integrate to produce a periodic variation of amplitude 28 ns in the
elapsed time recorded by the satellite clock. If it is not taken
properly into account, the eccentricity effect could cause an
unacceptable periodic navigational error of more than 8 m.
During the early development of the GPS, onboard computers had limited
capability. It was decided that correcting for the eccentricity effect
would be left to the receivers. Inexpensive receivers accurate to no
better than 100 m may not need to correct for the eccentricity effect.
But, for the best positional accuracy, receiver software must apply a
relativistic eccentricity correction to the time signals broadcast by
each satellite. The navigation message includes the current
eccentricity, orbital elements, and other information that the receiver
needs for computing and applying the eccentricity correction.”
[2]
The below diagram shows where these relativistic effects come into play.
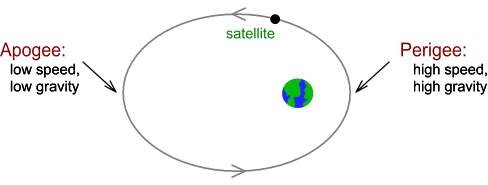
On the right side of the diagram is the perigee where the orbit is
closest, and the left side is the apogee where it is farthest.
(For visual ease the eccentricity is shown greatly exaggerated.)
The perigee has the highest speed and the lowest altitude.
So it should have high amounts of both motion-based and
gravitational-based time dilation.
The apogee has the lowest speed and the highest altitude.
So it should have low amounts of motion-based and gravitational-based
time dilation.
As a result, a clock in such an orbit would appear to run more slowly
at the perigee and more quickly at the apogee. Because
of this, receivers would need to make adjustments to the received clock
signals in order to calculate position correctly.
Another explanation?
The fact that adjustments need to be made within the receivers would
seem good evidence for relativity. Because, unlike satellite
adjustments, what goes on inside the receiver can be easily confirmed –
perhaps not by users, but easily enough by receiver manufacturers, of
which there are many.
So does this mean the eccentric adjustments have confirmed relativity
after all, or could there be another explanation?
In an earlier chapter on light it was proposed that
light moves through a vacuum with a speed that is added to the speed of
its source, i.e. at a speed c+v where v is the speed of the source
toward the target. This is known as the “ballistic” or
“emission model” of light.
Look again at the orbital diagram:
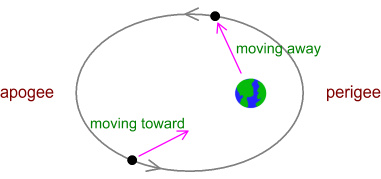
Note that as the satellite moves from the apogee to the perigee
(farthest to nearest point), it is moving toward Earth. So a
signal emitted during this phase would have the satellites’ speed added
to it and move at speed c+v rather than just c. It would
arrive sooner than “expected”.
Likewise as the satellite moves from the perigee to the apogee
(nearest to farthest point), it is moving away from Earth. So
a signal emitted during this phase would have the satellites’ speed
subtracted from it and move at speed c-v rather than c. It
would arrive later than “expected”.
Now if someone on Earth was under the assumption that the speed of the
signal must always be c, they would likely be confused as they see the
signals arriving earlier or later than their fixed-speed-of-light model
predicted. They might conclude that the satellites’ clocks
were somehow running at different speeds at different points in their
orbit. So this person would be working under an erroneous
assumption. And even though they would be able to use this
assumption to accurately predict the arrival times of signals, their
assumption would still be wrong.
Could it be then that this apparent periodic variation in clock rates
is in fact just a change in the transmitted signal speed?
Ballistic model analogy
To answer this we need to look at a simpler analogy. Consider
this classical mechanics situation:
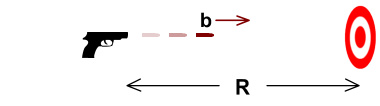
Here a gun aims at a target at distance R. The gun is
motionless with respect to the target and fires a bullet at velocity b
(relative to the gun). The bullet will take time T=R/b to
reach the target.
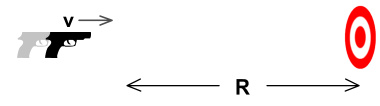
Now we change things a bit. In the above diagram, the gun
moves toward the target at velocity v (relative to the
target). When it is at distance R, it fires the
bullet. How long will the bullet take to reach the target?
The bullet now moves at velocity b+v (relative to the target) because
the gun’s velocity v is added to the bullet’s. Therefore it takes
time T=R/(b+v).
The difference between these times is:
ΔT = R/b – R/(b+v) = R v/(b (b+v))
For values of v much less than b, i.e. when the bullet moves much
faster than the gun, this closely approximates to:
ΔT ≈ R v/b2
Now translate the above to a satellite situation: replace the gun with
a satellite and the bullet with a radio signal moving at speed c
(relative to the satellite). Replacing b with c gives:
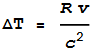 (1)
(1)
This tells us that the signal will arrive earlier by a time difference
proportional to distance and approaching velocity.
The calculated position error that would result from this time
difference (if one were assuming light’s speed must be c) is determined
by multiplying this by c. I.e.:
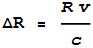 (2)
(2)
So how would this translate to a real situation? Let’s say a
GPS satellite had an eccentricity of 1%. The below graph
shows its relative velocity toward Earth.
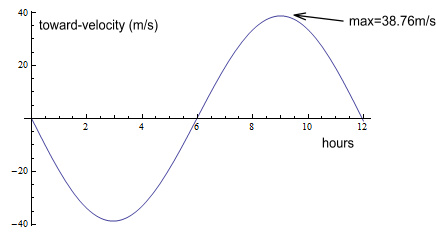
Here the horizontal scale represents time in hours over a 12 hour
orbit. Hour zero is the perigee (closest) and hour 6 is
the apogee (farthest). The vertical axis represents
velocity toward the Earth. As can be seen, the velocity
reaches a maximum of 38.76m/s on its approach and a minimum of negative
the same amount on its departure.
This next chart shows the change in radial distance over the orbit:
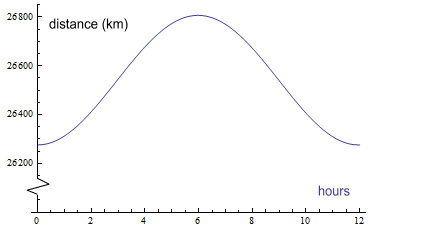
There is very little change, fluctuating by ±265km or 1% at most.
So what happens when we multiply these two charts in line with equation
(2)? We get this:
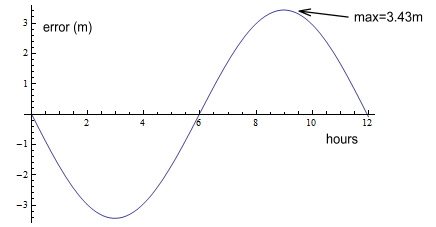
This shows the position error varies by plus and minus 3.43m.
This is almost half the 8m described in the referenced
article. In fact it turns out to be exactly half the
relativity-calculated amount.
The GPS Navigation User Interface guide gives the exact equation that is to be
used by receivers [3]. It is:
![\text{$\Delta $t} = -\frac{2 e\sqrt{G M A}}{c^2}\text{Sin}\left[E_k\right]](img/GPSm2-eqn3.gif) (3)
(3)
This corresponds to the amount of cumulative time difference due to
special and general relativity. e is the eccentricity, Ek is
the “eccentric anomaly”, which is the angle of orbit measured from the
centre of the ellipse, and G, M, and A are the
gravitational constant, Earth’s mass, and satellite’s semi-major axis respectively.
So what would be the equivalent equation due to changes in signal
speed? It works out to this:
![\text{$\Delta $t} = -\frac{e\sqrt{G M A}}{c^2}\text{Sin}\left[E_k\right]](img/GPSm2-eqn4.gif) (4)
(4)
Comparing this equation with (3), we see it has the same form but it is
exactly half the amount. Here is what a chart would look like
comparing them for a 2% eccentricity (e=0.02) and multiplying by c to
convert to position error.
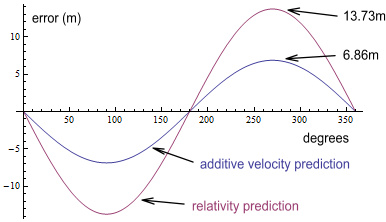
As can be seen, the prediction of relativity gives a maximum of 13.73m,
while the prediction due to additive velocity gives a maximum of
6.86m. So it would seem that additive velocities can predict
half the measured error. But since the receivers are
programmed to accommodate for double that amount, does that mean the
additive velocity idea is wrong and relativity is correct? Or
is the other half adjusted for elsewhere? We’ll get back
to that.
The Sagnac Effect
The other relativistic effect we apparently need to adjust for is the
Sagnac effect. The literature explaining this is somewhat
confusing so let’s ease into it with a couple of quotes:
The Physics Today article mentions:
“In the GPS, the Sagnac effect can produce discrepancies amounting to
hundreds of nanoseconds. Observers in the nonrotating ECI
inertial frame would not see a Sagnac effect. Instead, they would see
that receivers are moving while a signal is propagating. Receivers at
rest on Earth are moving quite rapidly (465 m/s at the equator) through
the ECI frame. Correcting for the Sagnac effect in the Earth-fixed
frame is equivalent to correcting for such receiver motion in the ECI
frame.”
While Wikipedia says:
“GPS observation processing must also compensate for the Sagnac effect.
The GPS time scale is defined in an inertial system but observations
are processed in an Earth-centered, Earth-fixed (co-rotating) system, a
system in which simultaneity is not uniquely defined. A coordinate
transformation is thus applied to convert from the inertial system to
the ECEF system. The resulting signal run time correction has opposite
algebraic signs for satellites in the Eastern and Western celestial
hemispheres. Ignoring this effect will produce an east-west error on
the order of hundreds of nanoseconds, or tens of meters in position.”
[4]
Based on this we can conclude that the Sagnac Effect:
- has to do with the rotation of the Earth.
- is most significant at the equator.
- is very important to compensate for because it can
result in “tens of meters” of position error.
We will now investigate a more detailed source by the same author here [5].
On page 8 is a calculation discussing sending signals around the
equator. It predicts a timing error of 207.4ns (equation
8). The calculation is rather complicated so let’s break it
into easier steps:
- If a signal was transmitted east along
the equator it would take 0.1337 seconds to get back to its starting
point (this could be done using mirrors or optic fibres for visible
light, or re-transmitters for radio signals). Calculation:
divide the circumference of the equator by the speed of light:
2*pi*6378137/(2.998x108) = 0.13367s
- But the equator is moving, and during
that time the original transmission point would have moved east by
62m. Calculation: multiply that time by equatorial velocity:
0.13367*465.1 = 62.17m
- It would take an additional 207.4ns to
cover that distance. Calculation: divide that distance by the
speed of light: 62.17/(2.998x108) = 2.074x10-7s = 207.4ns
At this point any rational person would have to be wondering: “What the
heck does this have to do with the GPS?” GPS satellites don’t
send signals around the equator!
When we read the words “Sagnac effect” it normally refers to light
travelling around a circle via rotating mirrors, such as this typical
laboratory-setup diagram shows:
Does this diagram resemble any portion of the GPS? Satellites
transmit their signal to Earth and that’s that. There’s no
transmission back to the satellites, or between satellites, and none of
their signals are made to loop the equator. So in what way
does the Sagnac effect have any relevance?
One place where the Sagnac effect would have relevance would be in the
synching of ground-monitoring stations. There are six
monitoring stations located roughly along the equator and these would
need to be kept in-synch with each other. Such a process
would need to adjust for the Sagnac effect, as the signal from the
designated master station was transmitted to the others.
But the documentation discussing the effect insists that it is also
relevant to GPS observers/users and that the receivers need to make
adjustments for it or they will calculate “tens of meters” of
position error. How to make sense of this, and what is the
207ns delay about?
Have a closer look at the motion of a satellite across the sky, this
time including the shape of Earth:
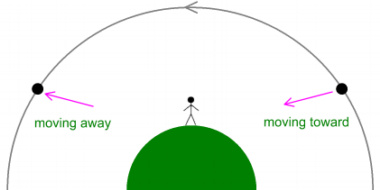
Here a satellite rises above the right horizon, passes directly
overhead a user, and goes down over the left horizon. As it
does so, notice that it spends time moving toward and away from the
user. This graph shows the velocity in a straight-line
direction, as viewed by the user:
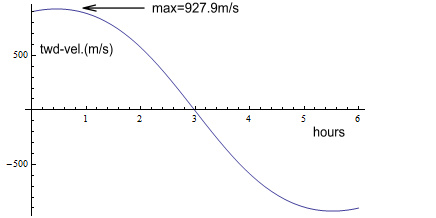
The velocity is zero when the satellite is directly overhead.
But as it approaches, the toward-velocity goes up to 927.9m/s, when
level with the horizon. And as it recedes, the velocity goes negative
by the same amount.
Returning to our earlier discussion on additive velocities, this could
mean the signal on the approach path arrives earlier than expected
because net velocity is higher, i.e. c+v. Likewise it could
take longer to arrive on the departing path because signal velocity is
lower, at c-v.
Could this be the explanation for the timing differences?
Satellites sit at an altitude of 20,184km. Plugging this into
equation (1) gives:
ΔT = R v/c2 = 20184000*927.9/(2.998x108)2 =
2.0837x10-7s = 208.4ns (5)
This is quite amazing as we have arrived at an almost identical number
as what the Sagnac-around-the-equator would predict! More
importantly it was arrived at using very different inputs.
The 207ns number used the equatorial circumference and
velocity. Whereas this 208ns number used the satellite’s
distance and velocity.
Could these additive velocities be the real cause of what is labelled
“Sagnac effect”? It does seem more logical, especially as
there is no reason why the Sagnac effect should have any relevance to
the communication between satellites and receivers.
Near the end of page 9 is a discussion about an experiment done to
measure the effect:
“In 1984 GPS satellites 3, 4, 6, and 8 were used in simultaneous common
view between three pairs of earth timing centers, to accomplish closure
in performing an around-the-world Sagnac experiment. ... The size of the Sagnac
correction varied from 240 to 350 ns.”
“240 to 350ns”? Shouldn’t that be “0 to 207ns”? The
effect is supposed to be due to Earth’s rotation, meaning it should be
zero at the poles. And how did it get up to 350ns when
207.4ns represents the maximum possible (at the equator)?
Refer to equation (5). Here the distance used for R was the
satellite altitude. This is only correct when the satellite
is directly overhead. In reality the satellite-receiver
distance will be larger when near the horizon. This graph
shows the actual distance as the satellite moves overhead.
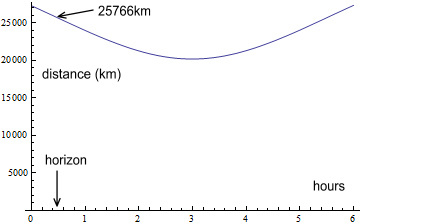
When level with the horizon, the distance is 25,766km. Using
that value in equation (5) gives a timing value of 266ns (207.4ns will
occur when the satellite is 29 degrees above the horizon).
This is above 240ns but still a fair way from 350ns. Perhaps
that 350ns reading was done on an aeroplane and the satellite in
question had an eccentric orbit. E.g. if the orbit
eccentricity was 1%, this would increase the maximum R value to
26,800km. And if the aeroplane moved at 245m/s (a typical jet
cruising speed [6]), we could add this to the 928m/s.
Plugging this into equation (1) gives a value of 350ns. Now
it is true that the reference didn’t say that one of the “timing
centers” was on an aeroplane, or that they were all fixed on the ground
for that matter. But how can they justify getting
350ns using the equatorial method?
We’ll look now at another reference here [7]. It appears to
be a more detailed version of the previous reference [5]. On
page 10 is a diagram that is reproduced below:
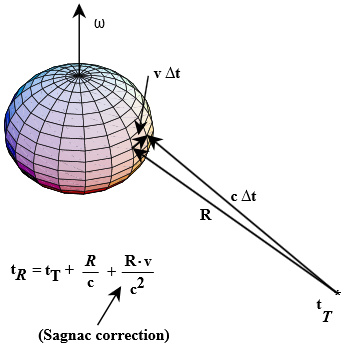
Notice there is a formula at bottom with the words “Sagnac correction”
pointing to one of the terms. This term looks identical in
form to equation (1), where R also refers to the distance between the
satellite and receiver. This is quite a change from the
previous reference where Sagnac corrections were calculated based on
the Earth’s circumference.
The only difference between this and (1) is that v refers to the
velocity of the Earth’s surface relative to its centre, rather than the
velocity of the satellite relative to the surface. But should
that be correct?
Taking the diagram at its word, the largest value of v will be the
equatorial velocity of 465.1m/s. The largest R would occur
when the satellite is on the horizon, which will be
R=25769km. Plugging this into the suggested “Sagnac
correction” gives:
v R/c2 = 465.1*25769000/(2.998x108)2 = 133.3ns
(6)
133.3ns? That is well short of the 207.4ns calculated using
the “equatorial circumference” method. Something fishy is
going on here!
On page 9 it gives the same equation (1.17) and equation 1.14 makes it
clear that R refers to the distance between the satellite (rT) and the
receiver (rR).
So what is v? In the paragraph above that it says:
“… and let the receiver have velocity v in the ECI frame.”
Where “ECI frame” means velocity relative to Earth’s centre, which
corresponds to the velocity described in the above diagram.
Logically however, v should refer to the relative velocity between the
satellite and receiver. After all, these are the components
that make up the GPS. The velocity of the receiver relative
to Earth’s centre should not be relevant, any more than the velocity of
the receiver relative to Jupiter could be relevant. Earth
just happens to be where the components are located. If we
were to relocate the satellites and receivers to Mars, there is no
reason why v should refer to Earth’s centre.
To understand this better, it would be helpful to refer to some
specific calculations. To do this we can refer to the User
Interface guide mentioned earlier [3]. Scanning this PDF for
the word “sagnac”, we find no mention of the Sagnac effect!
Quite amazing. On one hand we are told that the Sagnac effect
is important to adjust for otherwise it will result in “tens of metres
of error”. But the interface guide gives no specifics on how
to adjust for it, or even say that it needs to be adjusted
for. It should be also pointed out that this manual is what
GPS receiver manufactures are meant to rely on, so any necessary
adjustments would have to be described there.
Does this mean the “Sagnac effect” (or additive velocity equivalent)
adjustments have no relevance? I would say they do have
relevance, but have been left out of the main guide and sent separately
to manufacturers.
The reason for leaving out specific calculations might be to prevent
researchers from seeing that the velocity v refers to the relative
velocity between the satellite and receivers, rather than equatorial
velocity. And the reason for not wanting people seeing this
is that they might discover that the GPS shows that light’s speed is
not a constant speed c, as seen by all observers, but varies with the
speed of the source. Such a discovery would demolish the
fundamental postulate of Special Relativity.
It appears there are other things left out of the manual. For
example on page 113 a diagram says you need to compensate for
“Tropospheric Adjustments”. However there is no mention in
the guide about what adjustments to make (search the PDF for
“tropospher”). But we can find plenty of information on
the tropospheric adjustments elsewhere on the web e.g. by searching
“gps tropospheric delay”. Searching the gps.gov website
brings up 50 results over three pages [8].
By comparison, the only information available on the web for Sagnac
adjustments for GPS appears to be copies of Ashby’s papers.
Searching the gps.gov site for information on the Sagnac effect turns
up only three ‘powerpoint’-type visuals [9]. These say the
maximum is 133ns [10], which corresponds to equation (6). The
absence of detail on the Sagnac effect on the gps.gov website is
surprising to say the least!
Referring back to the Physics Today article [2], on page 46 is a column
“Confusion and consternation”. It talks about the problem of
adjusting for fast-moving receivers and says:
“One can estimate the discrepancies from the approximate
synchronization correction: v x/c2, where v is the receiver’s speed
through the ECI frame and x is its distance from the GPS satellite in
question.”
This looks similar to the “Sagnac” effect in equation (6). It
then says:
“Within the framework of general relativity, however, one coordinate
system should be as legitimate as another.”
That’s true, so why not make the receiver the reference frame and
describe v as the relative velocity between satellite and
receiver? It continues:
“Measurements made by an observer traveling with a moving receiver can
just as well be described in another reference frame, by using
transformations that relate the two frames. In the special case of two
inertial frames in uniform relative motion, these are the familiar
Lorentz transformations.”
This may be a clue. Transforming time using Lorentz
transforms uses the formula:
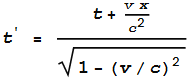 (7)
(7)
For values of v much less than c, the expression inside the square root
becomes very close to unity. So this is approximately:
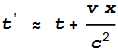 (8)
(8)
The expression on the right-hand side now looks like the
additive-speed-of-light adjustment in (1). It’s possible that
receivers manufacturers are told to make a Lorentz transform as shown
by (7) and this effectively gives them an additive-speed-of-light
adjustment.
It’s also possible that manufacturers are not given the specifics but
need to figure it out themselves. The column begins with:
“Historically, there has been much confusion about properly accounting
for relativistic effects. And it is almost impossible to discover how
different manufacturers go about it!”
If the interface guide had given specifics for handling the Sagnac effect
there should not be “much confusion” as manufacturers would go about it
the same way. Perhaps manufacturers do their own experiments and
end up settling with the Lorentz time transformation as shown in (7).
The TOPEX experiment
This brings us back to the earlier discussion about relativistic
adjustments for orbital eccentricity. In order to
resolve the question of reference frames, the Physics Today article
goes on to discuss an experiment that tested for the eccentricity
effects. It was done in space on a satellite called
TOPEX. This diagram is provided:
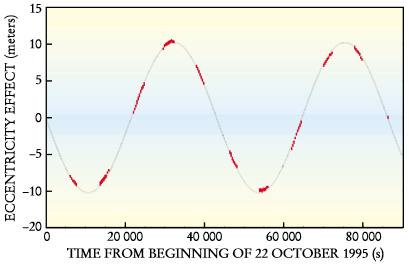
It shows the relativistic error for a GPS satellite with 1.5%
eccentricity. For an eccentricity of 0.015, this calculates
to a relativistic error of 10.3 metres, and this closely matches what
is shown in the diagram.
An obvious question arises however – why do this experiment in space
rather than on the ground? We have extremely accurate clocks
in many laboratories. If it were possible to do it on the
ground, then it could be verified independently. But if it
were not possible, then we can’t know whether the eccentricity effect
is due to relativity predictions or additive-speed of light
predictions. Instead we must take the word of those promoting
the relativity theory. This means the magnitude of the
eccentricity effect is questionable, just like the existence of the
38.6μs-per-day adjustments.
Conclusions
- There is no reason why GPS receivers
should have to adjust for a Sagnac effect. Various ‘official’
calculations for the effect are inconsistent with each other.
Whereas actual measurements don’t match the official calculations but
instead correspond to an additive speed of light. Information
on how to adjust for the Sagnac effect in receivers is strangely absent
in the official user guide and gps.gov website.
- The adjustment for orbital
eccentricity is quite likely not a relativistic adjustment but an
adjustment for a change in signal speed as the satellite moves toward
and away from the receiver. The difference between the
relativistic and the change-in-signal-speed predictions should be
measurable on Earth but for some reason is done in space where it can’t
be verified.
[1]
http://physicscentral.com/explore/writers/will.cfm
[2]
http://www.fing.edu.uy/if/cursos/fismod/GPS.pdf
page 45 (pdf page 5), or here
http://www.ipgp.fr/~tarantola/Files/Professional/GPS/Neil_Ashby_Relativity_GPS.pdf
[3] The user manuals are here:
http://www.gps.gov/technical/icwg/
This is the most recent version:
http://www.gps.gov/technical/icwg/IS-GPS-200H.pdf
See page 96, or 109 on the PDF
[4]
http://en.wikipedia.org/wiki/Error_analysis_for_the_Global_Positioning_System
[5]
http://relativity.livingreviews.org/Articles/lrr-2003-1/download/lrr-2003-1Color.pdf
pages 7-9
[6]
http://hypertextbook.com/facts/2002/JobyJosekutty.shtml
[7]
http://areeweb.polito.it/ricerca/relgrav/solciclos/ashby_d.pdf
[8]
A search for "troposphere" on gps.gov
[9]
A search for "sagnac" on gps.gov
[10]
http://www.gps.gov/governance/advisory/meetings/2011-11/nelson.pdf
page 14
|




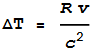 (1)
(1)


![\text{$\Delta $t} = -\frac{2 e\sqrt{G M A}}{c^2}\text{Sin}\left[E_k\right]](img/GPSm2-eqn3.gif) (3)
(3)![\text{$\Delta $t} = -\frac{e\sqrt{G M A}}{c^2}\text{Sin}\left[E_k\right]](img/GPSm2-eqn4.gif) (4)
(4)





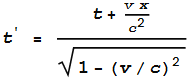 (7)
(7)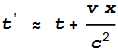 (8)
(8)