GPS, Relativity, and
pop-Science Mythology
Popular science frequently promotes
the idea that the Global Positioning System serves not only as a means
of position determination but also as a convenient test for Einstein’s
Theory of Relativity. The claim made is that if certain
adjustments were not made to counter the predictions of this theory,
calculated positions would quickly become very inaccurate.
Hence anyone with a functioning GPS receiver has already confirmed the
theory to be correct and the pizza delivery guy would not have arrived
at your home were it not for the adjustments.
The claim however is false and the science gurus who promote it should
know better than to do so. Fact is, it would not
matter whether such adjustments were made or not.
Why? The
reason has to do with basic facts about how GPS receivers work.
To understand this we first need examine the claims more specifically.
The following points are made in regards to Relativity and GPS
operation [1]:
- Relativity theory predicts the clocks
aboard the GPS satellites will run faster than clocks on Earth by about
38 microseconds a day.
- The satellites’ clocks are slowed down
by this amount so as to match the speed of clocks on Earth
- If these adjustments were not made,
position determination would be inaccurate by up to 11 km a day
- This inaccuracy would grow steadily
larger each day, e.g. after 10 days the inaccuracy would have grown to
110 km.
We’ll begin by assuming the first
two points are absolutely correct
since this essay is not about questioning the truth about relativity
theory, only its application.
Odd as it may sound, the third
and fourth points do not follow from the first two.
Determining your
position
The basics of how GPS receivers work
is fairly straightforward. An array of orbiting satellites
surrounds Earth. Each satellite holds one or more
highly-accurate atomic clocks. As they orbit, a satellite
transmits the time signal (or ‘timestamp’) of its on-board
clock. Since these
signals travel at a finite speed – the speed of
light – we can
determine how far away each satellite is from the receiver and thus
figure out where we are located.
Calculating the distance from a satellite requires subtracting the time
signal of the satellite from the time at the receiver. By
subtracting these numbers and multiplying by the speed of light we
calculate distance, i.e.
D = (tr - ts) c
Where tr is time at the
receiver, ts is the (delayed)
time signal from
the satellite, and D
is distance. By determining the distance
from at least 4 satellites we can pinpoint our location.
This calculation is generally drawn in
terms of a set of overlapping spheres:
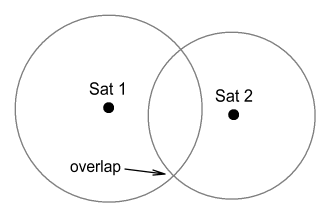
In three dimensions, our position
will be given by the
intersection of four such spheres.
Now here’s where time dilation comes in. If the clocks on
Earth ran at a different rate to those on satellites then the above
calculation would be completely out because |tr-ts| would become
increasingly larger each day. We can calculate the daily
distance error δD
by multiplying the daily time error δt by the speed of
light:
δD = δt c
~= 38x10-6
* 3x108 = 11400 m
Or about 11 km per day.
This argument appears quite solid. So what are we overlooking?
What we are overlooking is the phrase ‘time at the receiver’.
Problem is, GPS receivers contain no atomic clock because there’s no
room to fit one in. Plus it would be very expensive even if
possible. That ‘time at the receiver’ must instead be
determined from the satellites’ clocks. Therefore if the
satellites’ clocks were running faster (or slower) than those on Earth,
this ‘time at the receiver’ would likewise run faster or slower by
exactly the same degree. Hence there would be no position
error
due to time dilation, and certainly no cumulative position error.
Essentially, what the GPS receiver is trying to determine is not just
its position but also its timestamp. To state this
mathematically, it is trying to determine variables x,y,z, and
t.
That’s 4 variables which require 4 pieces of data to solve
for, and the data for solving it comes from the timestamps of 4
satellites. The receiver computes all 4 of these variables
x,y,z,t but then can discard the time variable (t)
as unimportant.
A simpler approach
Putting aside whatever method it is
that GPS receivers actually use,
there is a much simpler approach to calculating position that sidesteps
the whole ‘time at the receiver’ question and makes it clear why the
clocks’ speed relative to Earth is unimportant. It involves
comparing differences between received signals.
Let’s say you are at an unknown location on Earth (or in space) and you
receive two identical signals from different satellites. That
is, the timestamps from each satellite are exactly the same when they
reach you. What would you conclude from this? Quite
obviously: that you are at a position equally distant from both
satellites. Therefore you must be somewhere on a plane that
slices midway between the two satellites and runs at right-angles to a
line joining them. Using this information you have narrowed
your location down to a two-dimensional plane. And you did so
without knowing your local time. Now quite obviously also, it
wouldn’t matter if those satellites’ clocks were both running faster or
both running slower than yours because your equidistance makes their
timestamps identical when they reach you.
That much is straightforward. So what about a situation where
there is a
measured difference between time signals, as will
normally
be the case? In this case it is slightly more complex but
again the answer will depend only on the difference between the signals
rather than any local clock’s time.
To simplify this, suppose we have a two-dimensional situation
containing three satellites: A, B and C. All satellites are
at known locations with their clocks perfectly synchronised and running
at identical
speeds.
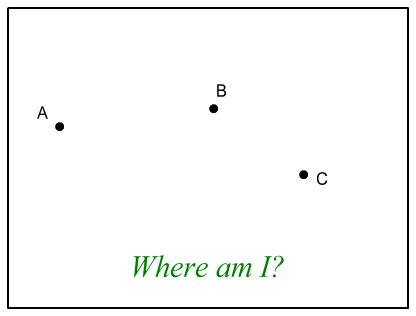
We are somewhere in this 2D region
shown and wish to determine our
position. We receive signals from A and B, and find that B is
slightly ahead of A. We subtract the time difference between
these two signals and call it Δt.
What this tells us is
that we are closer to B than A, and at a location where the difference
between our distance to A and our distance to B is c Δt.
Putting aside the math, this places us somewhere along a line looking
like this:
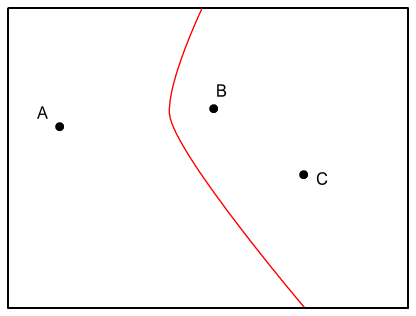
The line looks a bit like a
parabola, although it isn’t [2].
Next we look at the signals from B and C and find they are
identical. As discussed above, this places us on a straight
line running midway between B and C like so:
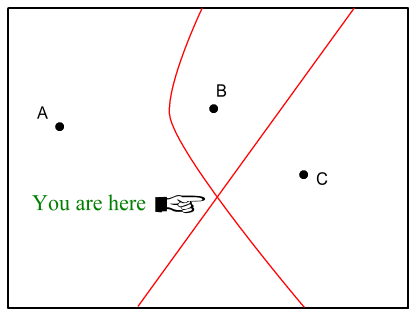
Where these two lines intersect,
that’s our position!
The above is a two dimensional situation. Extending it to
three dimensions will require four satellites and the intersection of
three overlapping ‘parabolic’ cones. A little more complex
but the method is the same.
The important point here is that we were able to determine our location
without making any reference to ‘local time’. Doing so only required
knowing of differences between satellite timestamps rather than the
timestamps themselves. So long as the satellites’ clocks all run at the
same rate, these timestamp differences will be independent of the actual
clock speeds.
That last point might be confusing. After all, if I double
the speed of two clocks
won’t that also double the magnitude of their difference?
Short answer: no. To easily demonstrate we’ll take two simple
bench clocks, labelled A and B, and set one 10 minutes ahead of the
other. We’ll start our experiment when clock A reads 1:00
and clock B reads 1:10. We’ll then observe them every 5
minutes and compare them to ‘real time’, which in this case will also
be clock A’s time.
| real time |
1:00 |
1:05 |
1:10 |
1:15 |
| clock A |
1:00 |
1:05 |
1:10 |
1:15 |
| clock B |
1:10 |
1:15 |
1:20 |
1:25 |
OK, no surprises there: B stays always 10 minutes ahead of
A.
Now we redo the experiment but this time make an adjustment to both
clocks so as they run at double their normal speed. That is,
for each one minute of real time, A and B move ahead 2
minutes. We again start the experiment when A = 1:00, B =
1:10 and observe them every 5 minutes.
| real time |
1:00 |
1:05 |
1:10 |
1:15 |
| clock A |
1:00 |
1:10 |
1:20 |
1:30 |
| clock B |
1:10 |
1:20 |
1:30 |
1:40 |
So the clocks move at double the rate of real time but keep the same
10 minute difference as before.
The above experiment could instead be done by having A and B set to the
same time and then sending B 10 light-minutes away – about double the
Earth-Mars distance. In this case a time signal from B would
take 10 minutes to reach here, meaning that its signal would read 10
minutes behind A. Using the same reasoning as above it should
be clear that doubling the speed of both clocks would not change the
observed time difference (of 10 minutes) between the two. The
same goes for GPS satellites. Whether they run faster or
slower than our clocks, it will not alter their measured time
differences. And hence our GPS-calculated position will be
the same.
Determining a
Satellite’s position
Now admittedly there is an aspect in
which relativity can
become relevant. And this has to do with figuring out where a
satellite is.
The above exercises assume the satellites to be at fixed locations,
which is not the case. The satellites are of course in orbit,
changing position all the time, and it’s up to the receivers to
determine their location. This calculation will be based on a
satellite’s orbital characteristics (which are also transmitted) and
its timestamp. Essentially the timestamp allows us to
determine how far around in an orbit a satellite is.
Therefore any inaccuracy in a timestamp – such as a relativistic
slow-down – will cause an inaccurate position to be calculated.
Fortunately such inaccuracies will be mild because the satellites move
much slower than light. The satellites move at 3870m/s and
a 38.6 microseconds-per-day inaccuracy would yield a position error
of only 15cm. Naturally this will accumulate as the days go
by, but the orbital times are calculated relative to a ‘reference
epoch’ which is reset weekly and the regular timestamp extends plus or
minus 3.5 days from this reference time [3].
Hence the
satellite’s calculated position could be out by up to 52cm, which is
still within the normal GPS inaccuracy of 2-3 metres. And
since satellites are moving in different directions even this error
should largely cancel; especially when averaged over several readings.
Latitudes and Altitudes
Ignoring all the above arguments for
the moment, there is another
important consideration that warrants attention. And that is
the fact that such relativistic effects would render the entire
navigation system unworkable, at least in its present
configuration. According to the US-DOD [4]
the satellites
lose 7200 ns a day due to special relativity and gain 45900 ns a day
due to general relativity. These effects combine to yield a
net speeding up of 38600 ns a day (45900-7200=38600), relative to clocks
on Earth. The clocks are then slowed by a suitable degree to
negate this daily amount, and everything is fine for GPS receivers.
However since the Earth is rotating, the speed of a satellite relative
to a GPS receiver will be different at different latitudes.
Therefore the amount of dilation should also be different.
That 7200 ns was calculated relative to a pole, where the Earth is not
moving and only the satellite’s speed of 3870 m/s need be
considered. If the calculation was done at the equator where
the surface moves at 465 m/s and GPS satellites cross at 55 degrees,
the SR time dilation works out to 6300 ns. That’s a 900 ns
difference between pole and equator which presumably would yield an
increasingly inaccurate position determination of 270 meters per day.
Next we have a problem with altitude because the 45900 ns figure was
calculated for sea level. This figure will decrease as we
move higher and experience less gravity. For example, at 1060
metres above sea level there will be a decrease of 10 ns per
day. This presumably would lead to an inaccuracy of 3 metres
per day, accumulating up to 1 km per year. Aeroplanes flying
at 10km would be worse off; accumulating a 10 km error per year.
If it were necessary to accommodate for relativity at different
latitudes and altitudes, the calculations would be very complex and
would need to be done at the receiver. But they aren’t
done there: only a fixed time adjustment is made at the satellites for
all points on Earth. This fact alone demonstrates that
Relativity is irrelevant to the GPS operation.
Conclusion
The presence of Special and General
Relativity effects has no bearing on the accuracy of GPS
operation. In summary, it wouldn’t matter whether clocks
aboard GPS satellites ran faster or slower than Earth’s clocks or even
changed their speed each day. Just so long as the satellites’
clocks remained synchronised with each other and the time-difference
relative Earth’s clocks didn’t become too large, GPS receivers would
continue to calculate their correct position.
The GPS is certainly an excellent navigational aid. But from
an operational viewpoint at least, it doesn’t serve as a test for
Relativity. Scientists should stop calling it that.
The next chapter discusses ‘secondary relativistic effects’:
GPS Mythology - part 2
(<-- click to read)
[1]
http://en.wikipedia.org/wiki/Error_analysis_for_the_Global_Positioning_System
[2] The shape
looks like the
function y=sqrt[1+x2]
[3]
http://www.navcen.uscg.gov/pubs/gps/sigspec/gpssps1.pdf
PDF-page 43
[4]
http://www.aticourses.com/global_positioning_system.htm
|



