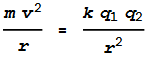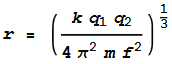The Photoelectric Effect
When light hits a metallic surface under suitable conditions we can
observe electrons being ejected. This is called the
Photoelectric Effect and was first studied by Hertz and J.J. Thompson
in the late 1800s.
The fact that this happens this should probably come as no
surprise. Light carries ‘energy’, which is to say it can
cause electrons to move about and a surface to heat up.
Presumably then, it should occasionally cause electrons to be ejected
altogether.
A closer examination into the effect however reveals some unexpected
behaviour:
- Increasing the intensity of the light
increases the number of ejected electrons per second, but their
ejection speed (kinetic energy) remains the same.
- Light below a certain frequency ejects
no electrons at all. Whereas light above that threshold
frequency can eject electrons, even when the light’s intensity is low.
- The ejection speed of electrons appears
to be a function of frequency, such that an increase in frequency
brings about an increase in speed.
- This threshold frequency is different
for different materials, and different materials have different
ejection speeds.
- The effect is seemingly immediate and
doesn’t require the energy to be built-up over a period.
In response to this, and building on the work of Plank, Einstein
postulated that light consists of discrete units, or ‘quanta’ of
energy. These units were later called photons, and the energy
of each photon was said to be in direct proportion to its underlying
frequency. So in order to remove an election from
an atom, i.e. to ionize it, the frequency of the photon must first be
above the atom’s ionizing energy. Otherwise the electron will
stay put, regardless of how many photons rain down on it.
Under this proposal light took on a split personality; behaving
sometimes as waves and other times as particles, depending on the
experimental setup. For example when producing interference
patterns, light is considered a wave. But for the
Photoelectric effect and a related one called Compton scattering, it is
considered a particle. The contradictory nature of this
proposal led to an ongoing debate over light’s dual wave/particle
nature that continues to this day.
Another approach?
There is however a much simpler approach to explain what’s happening
here, without having to postulate that light behaves both as a wave and
a particle. In fact when properly considered, what is
observed is what we should logically expect from the classical orbital
model of an atom.
Before getting to the details on this, it should be pointed out that
the claim that low-frequency light can’t ionize an atom is
incorrect. One method of ionizing atoms is to expose them to
a powerful electric field. This can be done for example by
applying a high voltage across opposing metal plates, giving rise to a
static electric field between them. Now technically speaking,
a static (fixed) electric field is light of zero frequency.
Presumably this means that field has zero energy and nothing should
happen. But with enough voltage, electrons on the negative
plate will be removed and jump across to the positive plate.
If done in air, this will result in a spark.
Another example would be the giant CO2 lasers used in an unsuccessful
attempt to produce hot fusion. These lasers use frequencies
in the infrared range, which is much lower than what the photoelectric
effect would require (usually ultraviolet). And yet these
intense low frequencies can ionize a substance into plasma, completely
removing all of its electrons.[1]
So clearly, given enough intensity, low or zero frequency light can
remove electrons.
But putting aside situations involving ultra-intense amplitudes, it is
true to say that frequencies below a certain level will be unable to
remove electrons above a certain ‘energy level’.
The opera singer
To understand this, consider a tale that is sometimes told of an opera
singer and a wine glass. As she sings, the glass vibrates.
Then, just as she hits the right note, the glass vibrates so much it
shatters. This feat has been demonstrated by a number of singers,
although is much easier to do with electronic sounds and amplifiers.
How does it happen? The process is called ‘resonance’ and is
due to ‘natural frequencies’. All objects vibrate when
exposed to sound. And they do so more strongly when the
impacting frequency corresponds to a natural vibrational frequency of
the object in question.
Another example would be a piano. When a separate instrument
plays a note, the piano string corresponding to that note is observed
to vibrate. This is called ‘sympathetic vibration’ and is
also due to natural frequencies.
The frequency of planets
Now consider the Solar System. Our Sun is surrounded by a
number of planets. Each planet orbits in a roughly circular
path, and with different orbital period. The closest planet,
Mercury, orbits once every 32 days. While the furthest
planet, Neptune (as now defined), does so once every 273 years.
Instead of describing planets according to orbital periods, we could do
so in terms of frequency. For example we could specify how
many times they orbit the Sun every 1000 years.
Under this description, Mercury would have a frequency of 11,400 (orbits
per 1000 years), Earth would have exactly 1000, and Neptune’s frequency
would be 3.67. So the inner planets have the highest
frequencies, and the outermost the lowest.
Orbital frequencies of electrons
This planetary model is rather similar to the early Bohr model of the
atom. In Bohr’s model, electrons circle the nucleus at
differing distances. The inner electrons orbit at high
frequencies, and the outer electrons at lower frequencies.
Now for an important question: What would happen if we
exposed that atom to an electromagnetic wave who’s frequency matched
the orbital frequency of one of its electrons?
Let’s first consider the impact of a fixed electric field.
That is, light of zero frequency. What will happen?
If the field is weak, the atom’s (positive) nucleus will be pulled in
one direction, and it’s electrons in the other. The result
would be an electron in an elliptic orbit.
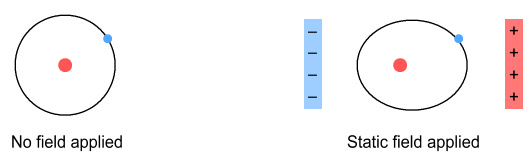
If the applied field was strong enough, it would pull the electron
completely away, ionizing the atom.
Now consider the impact of a low-frequency wave, i.e. light with
frequency lower than the electron’s orbital frequency. As it
impacts, the wave pushes the electron ‘to-and-fro’: sometimes in the
same direction as what the electron is moving, and other times in the
opposing direction. Or if you prefer, sometimes pushing it
toward the nucleus and other times away.
As a result the orbit is shaken up but not enough for it to
break. Once the incoming wave stops, the orbit returns to its
previous circular path.
Now consider the situation where the input frequency matches the
orbital frequency. Initially there might be some ‘confusion’
as the incoming wave pushes and pulls in the opposing direction to what
the electron is moving. But after a short while the orbit
will ‘phase lock’ or synchronise with the incoming wave.
The situation is now somewhat different from the preceding
example. Here the incoming wave pulls on the electron in an
outward direction (away from the nucleus) during both ‘halves’ of the
orbit.
The incoming wave in now at the ‘natural frequency’ of the electron’s
motion. Just like the wine glass, the orbit experiences so
much force it is ‘shattered’. Or rather, the electron is
pulled away from the nucleus where the attractive force is reduced.
At this point the existing speed of the electron takes over and enables
the electron to fly fully away from the nucleus. The atom is
ionized. From an observer’s viewpoint it might appear that
the incoming wave ionized the atom because the light’s frequency had
the right ‘energy’. But in reality it did so because it
matched the frequency of the orbit.
What about higher frequencies?
The above describes a situation in which an electron can be ejected
when the incoming wave matches the frequency of the orbit. So
what about the situation where the wave frequency is higher than the
orbit frequency? In this case the wave is no longer at the
natural frequency and thus shouldn’t be able to eject the
electron. Except we know it does.
To understand why, look again at the Solar System. Here we
have many planets orbiting at different distances from the
Sun. The inner planets have the highest frequency and the
outer planets the lowest.
An atom is a similar situation. There are inner electrons
orbiting at high frequency and outer ones at low frequency.
When a high frequency wave comes in, the outer electrons might not be
very affected. But the inner ones will be. When an
incoming wave matches the natural frequency of an inner electron, that
electron will be ejected.
So how does this affect the outer electrons? There are two
possibilities to consider. The first is that, in the process
of being ejected, the inner electrons would pass through the orbits of
the outer electrons. This might destabilise their orbits to
the point that they also got ejected.
The second and more likely scenario is that once the inner electrons
got ejected, the outer electrons would drop in altitude to fill the
newly vacated orbit space. Once there, the electron that took
up the old orbit would have the frequency of the incoming
wave. It too would be ejected and another electron would drop
to fill that vacancy. This process would continue until
electrons of (originally) lower frequency (and higher altitude) were
also ejected.
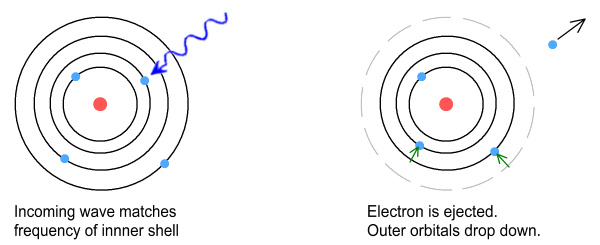
Thus a high frequency corresponding to an electron in an inner orbit
ends up ejecting all the electrons from the outer orbits.
Another thing that should be apparent is that higher frequencies
correspond to higher orbit speeds. And so an
electron ejected from a higher orbit speed should be expected to leave
the material surface faster. This is consistent with the
observation that higher frequencies eject electrons at higher energies
(speeds).
It should also be noted that this ejection process would be quite
fast. I.e. it should happen within a few cycles of
the incoming wave. So to us it would appear
instantaneous. This is consistent with the observation that
the photoelectric effect is immediate and doesn’t require a build-up of
energy before an electron is ejected.
A simple test
In order to test the validity of this theory we need to ‘plug some
numbers in’ to see how it matches the real world. We can look
at oxygen as an example. Oxygen is ionized with ultraviolet
light of frequency of 3.3x1015 Hz (or wavelength 91nm) [2].
What electron orbital radius does that correspond to?
Oxygen has 8 protons in the nucleus and as many electrons on the
outside. So each electron could be considered as orbiting a
single proton because the positive field from the other 7 protons would
be effectively cancelled by the negative field of other 7
electrons. This leaves us with a very simple model of an
electron orbiting a proton. So the question is, how far from
the proton would an electron need to be to orbit 3.3x1015 times a
second?
To do this we need to find out when the outward centrifugal force
matches the inward Coulomb force. This will happen when:
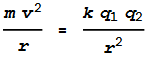
The left side of the equation is the centrifugal and the right side is
the Coulomb. We can substitute velocity v with v=2 pi r f,
where f is the orbit frequency. Isolating the radius term
gives:
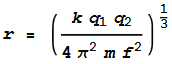
Substituting in values: k=9x109, q1=q2=1.6x10-19 C, m=9.1x10-31
kg, f=3.3x1015, gives:
r= 8.4x10-11m or 84pm
Oxygen has a ‘Van der Waals’ radius of 152pm. These numbers
are very close – arguably too close to be put down to
coincidence. It thus shows that the explanation given here
for the photoelectric effect is likely to be correct. The
difference between these numbers can be attributed to (a) the
orbit model being simplistic and (b) the Van der Waals radius being
an approximation of the outer orbit shell size. For a closer
match we could also look at oxygen’s covalent radius, which is listed
as being 66pm.
Related effects
Finally, it should be mentioned that the ionizing process being described
here doesn’t just apply to the photoelectric effect, i.e. where electrons
are ejected from metals, but also to light-induced chemical reactions.
For example, exposing skin to ultraviolet light can cause sunburn.
But strong infrared light will cook you rather
than give a tan. Actually it needs to be a high-frequency
ultraviolet because a UV ‘black light’ won’t cause sunburn
either. This tells us the frequency needs to be above a
certain critical point for skin to be damaged in a manner consistent
with sunburn. This frequency probably corresponds to
outer-shell electrons of similar frequency being removed, causing
chemical bonds to be broken.
Another example would be photosynthesis, in which plants use
ultraviolet light to convert carbon dioxide and water into
sugar. Apparently light in the low-frequency visible portion
of the spectrum is unsuitable for the task, even when
intense. Again, this is likely due to electrons in the outer
orbits of carbon and oxygen having a frequency in the ultraviolet
range, and the CO2 bonds won’t be broken until certain outer-shell
electrons are removed.
[1] http://en.wikipedia.org/wiki/List_of_fusion_experiments
[2] The ionizing energy
of oxygen’s outer shell is 1313.9 kJ/mol.
Multiplying by 1000 and dividing by Avogadro’s
constant gives us 2.18x10-18 J. Dividing this by Plank’s
constant gives a frequency of 3.29x1015 Hz.
|