Muons and Relativity
A muon is a type of subatomic particle that is created in particle
collisions. More properly called a “mu-meson”, it has a
charge equal to that of an electron and a mass 206 times
heavier. As such it is often thought of as a heavy electron
[1].
Unlike electrons however, muons are short lived and will quickly decay
into other particles, typically an electron and some
neutrinos. Laboratory experiments show that their average
life span (or rather half-life) is 2.2 microseconds. That is,
if we start with 1000 muons, after 2 microseconds we would expect
around 500 to remain. Then after a further 2 microseconds,
250 will remain, then 125, etc.
Muons are also created at high altitudes where the top of the
atmosphere gets bombarded by solar and cosmic protons. The
generated muons rain down at high speed, some of them decaying partway
down and others making it all the way to the ground at sea level.
According to our knowledge of decay times, we should expect the average
distance they travel before decaying will depend on their initial
speed. For example if a muon were going at 50% of light
speed, we’d expect it to travel (on average) 300 metres before decaying
[2].
Based on this we should expect the number of muons detected at that
300m distance to be half of the original. And at 600m down we'd
expect a quarter of the original to remain, at 900m one eighth would
remain, etc. We can continue this down to sea level and determine
what percentage would survive based on their original velocity.
Now it is noted that the number that make it to sea level is somewhat
greater than what might be expected. In fact the number that
make it the ground is more than should be possible even if muons were
assumed to be travelling at light speed (where the average decay
distance calculates as 600m).
However, if we take into account the predictions of Special Relativity
(SR) in which “moving clocks run slow”, we should expect muons moving
at high velocity be time-dilated and thus decay more slowly. In
this way a muon would move a farther distance before terminating.
Most interesting though, is the actual counts of muons do indeed appear
to match the amounts predicted by SR. For example, muons going at
0.87c, where the Lorentz factor is 2, travel twice the distance before
decaying. And muons going at 0.995c, where the factor is 10,
travel 10 times the distance before decaying.
This experiment would appear to be very good evidence for SR.
Because if we consider a muon to be a clock, it shows that its decay
time is directly influenced by its speed relative to Earth and by the
degree calculated according to SR.
But at the same time this explanation could also not be correct
because speed is relative: From the point of view of the
atmospheric muon, it is standing still, and muons on the ground are
moving. And so the ground muons should be decaying more
slowly instead.
This point should be immediately obvious but apparently it
isn’t. So it’s worth detailing the issue with a ‘thought
experiment’ as follows.
Choose two locations; one at ground-level and the other at
2000ft. There is an observer at both places, each with a
convenient box in hand. We place a flashbulb at the
mid-point, i.e. at 1000ft. The flashbulb is lit and gives off
a brief pulse.
When the observer at the 2000ft altitude sees the flash, he quickly
places the box around a group of a hundred muons that just happen to be
passing by and in the downward direction at exactly 0.995c.
The box is given a quick downward push so that it matches the 0.995c
velocity and heads down with the muons, without making contact with any
of them.
When the observer at the ground-level altitude sees the flash, he quickly
places the box around a group of a hundred muons that he finds sitting
stationary just above the ground (assume these muons aren’t affected by
gravity). The box and muons then stay at that level without
moving.
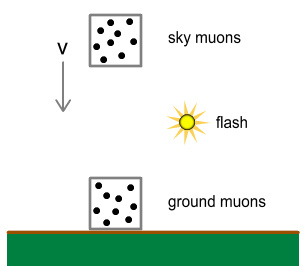
A box containing muons coming down from the sky is
approaching a similar box on the ground. An equal number of muons
were boxed at the same time.
The flashbulb ensures both groups were boxed simultaneously
(this is also an accepted method in SR of
synchronizing two clocks at a distance [3]).
The muons boxed at 2000ft were going at 0.995c. So according
to SR, they will decay 10 times more slowly than the (stationary) ones
at ground-level. Therefore when the boxes meet side-by-side at
ground-level, we should expect there to be more muons in the
“sky box” than in the “ground box”.
But according to the muons boxed at 2000ft, they are motionless and the
muons at ground-level (along with the Earth) are rushing upward at
0.995c. From their perspective, muons at ground-level will be
decaying 10 times slower. Therefore when the boxes meet
side-by-side, we should expect there to be more muons in the ground-box
than in the sky-box.
Clearly this is a contradiction as each box is required to contain more
muons than the other! To make this more explicit, suppose
that shortly after the muons are boxed, everything else ceases to
exist. The universe now consists solely of two identical
boxes containing 100 muons heading toward each other. When
they meet, which box will contain fewer muons? On what
grounds do we favour one over the other? Placing the Earth
back into the picture should not change anything SR-wise, and so the
question remains the same.
Therefore in order to solve the question of why the “moving muons”
outlive the “stationary muons”, it will be necessary to explore other
possibilities.
One possibility is that the muons coming down through the atmosphere
are not going just under light speed, but somewhat faster. In
this way the muons will travel a greater distance before
decaying. E.g. a muon going at double light speed will travel
1200m before decaying, a muon going at 10c will go 6000m, etc.
This possibility would likely strike the relativity supporter as
absurd. So much so, that they would probably not even
consider it in the first place. One reason for this has to do
with conditioned thinking. Another (more scientific) reason
though is because the speed of the muons has already been measured and
seen to be less than light. But is that really the case?
To understand this, it is recommended to watch this video showing the
famous 1962 “Frisch & Smith” experiment on muon (mu-meson)
decay. It is rather long but quite well presented:
youtube.com/watch?v=tbsdrHlLfVQ
In summary, muons are created at the top of the atmosphere and come
down at a range of speeds; some slow, some fast. What the
experimenters need to do is ‘filter out’ the slow muons so that only
the very fast ones are measured. The way they do this is to
put a large block of iron above the detector. This slows down
the muons. The slow ones will come to a stop and decay inside
the iron block before reaching the detector. Only fast muons
will make it to the other side and get detected. The
thickness of the iron block will determine the minimum speed of what
gets through. In the experiment it was built at 2.5 feet
thick, and this apparently let through only muons that were originally
going at 0.9950c (99.5% the speed of light) or faster.
The muons that make it through the block it then pass through a
cylinder of clear plastic called a ‘scintillator’. The
purpose of the scintillator is not just to detect the particles but
also to filter out anything faster than a certain speed. The
thickness/depth of the scintillator determines the upper speed
limit. In this case they set it so that the original upper
speed (prior to reaching the iron block) is 0.9954c. Anything
beyond that passes through the scintillator before it can decay and
give off a flash of light that they can observe. So what we
end up looking at are muons in the range of 0.9950c to 0.9954c.
Now it is true to say that, once in the scintillator we can measure the
muon’s speed because we have a distance and a time. But keep
in mind that the muons at this point have been slowed down from their
original assumed speed of 0.995c and are now going much
slower. Based on the fact that some of them decay within the
cylinder (in 2 microseconds) and the cylinder looks 60cm deep means they
must now be going 300,000m/s, or 1000 times slower than light at that
point. So we can’t use the scintillator to measure the
original speed, only the slowed-down speed.
So the real question is, how did they determine the original 0.995c
speed? They describe this at 22:00 but don’t give enough
detail. So I’ll try do so here.
As charged particles (such as muons) move through the iron they
experience a drag force. To simplify this, let us suppose
that the force is of known fixed strength while the muon is in motion,
and stops when the muon stops. The following diagrams
describe the situation:
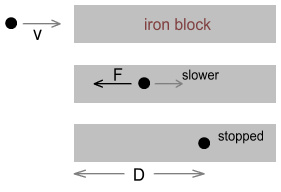
- In the top frame, a muon is coming from the left at velocity v and is
about to enter the iron.
- In the middle frame, the muon is passing through the iron and
experiencing a steady backward force of F. Because of this,
its velocity steadily decreases.
- In the bottom frame, the muon has come to a halt after travelling
distance D.
So how do we determine how far it travels before stopping?
This can be done using energy conservation equations.
The muon strikes the iron with a certain amount of kinetic
energy. As it passes through, this energy gets steadily
converted to potential energy according to the equation:
Energy(potential) = force * distance
If the muon comes to a stop, this means the original kinetic energy of
the muon has been fully converted. As you probably know,
kinetic energy is given by the equation:
E(kinetic) = ½ mass * velocity2
By setting these energy equations equal we can determine the stopping
distance from a known initial velocity. Alternatively, if we
know the stopping distance, we can instead determine the initial
velocity. I.e. we can determine how fast the muon was going
when it hit the iron. And this is what we are trying to
figure out in this situation.
The ½ m v2 equation however is for classical mechanics.
There is another equation that is used in relativity. It is
of the form:
E(kinetic) = Erelativistic – Erest
= E – E0 = m*c2 – m0*c2
Where m0 is the rest mass and m is the relativistic mass. m
is equal to m0/sqrt(1-v2/c2),
i.e. the rest mass multiplied by the Lorentz Transform.
What is the difference between these two functions? For
low velocities there is basically no difference. But for high
velocities, the velocity calculated by the classical formula can allow
v>c. Whereas the relativistic formula ensures
v<c.
The above is simplified. In reality the force experienced
won’t be constant but a complicated function of velocity. The
actual function used is called the Bethe Formula. A summary
is here:
en.wikipedia.org/wiki/Bethe_formula
Notice there are two versions: a non-relativistic one for low
velocities (eqn. 2), and a relativistic one for high velocities (eqn.
1). The relativistic one contains the Lorentz Transform.
So which equation do you think they use? If you are a believer
in relativity you will use the relativistic equation, correct?
Otherwise you will get a result that is inconsistent with relativity,
and therefore not considered a proper test of relativity.
But by using the relativistic energy equation you get different results
for v. And you guarantee v<c. Whereas using
the classical equation can give v>c, especially for high-energy
situations. But this possibility is immediately rejected
because everyone “knows” it’s not possible. In fact, it is
usually not even considered.
So the experiments for muon decay unknowingly end up with the
sqrt(1-v2/c2) function built into the outcome. And thus, no
surprise, “confirms” the function to be true!
Direct measurement of speed
Muon speeds can also be directly measured by timing how long it takes
them to pass between two locations. Experiments that employ
this method report that the maximum speed recorded is always less than
light. On the face of it this would appear good evidence that
muons, and presumably other particles, are restricted by a light-speed
limit.
A closer inspection of the experiments however reveals that what is
being reported is not the maximum speed of individual muons but the
average speed of many.
Take this reference for example [4]. It’s an experiment that
measures how quickly muons move between two flat horizontal detector
paddles located one above the other.
The below charts were reproduced from Figure 5. It shows the
results of multiple recorded speeds.
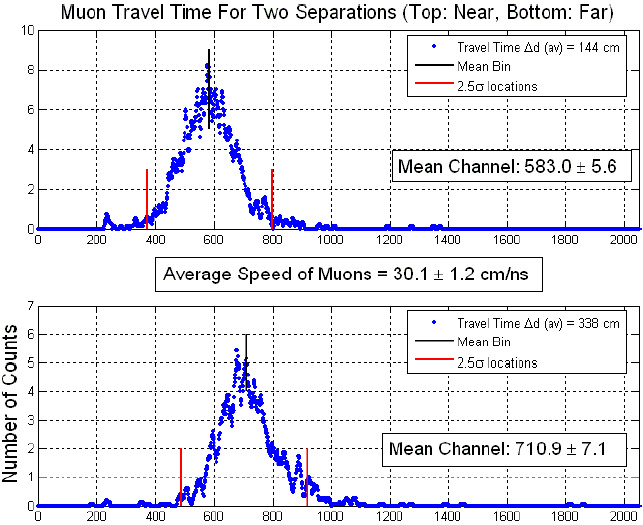
If we look at the top chart, it shows the average occurring around
channel 583, which corresponds to 30.1cm/ns and is close to the speed
of light (30cm/ns). But the range shown within the red lines
(within 2.5 standard deviations) goes from 380 to 800. That
would suggest a speed range from 583/800c= 0.73c to
583/380c= 1.53c
Actually the lowest channel where an event occurs appears to be 220,
and this translates to 583/220c= 2.7c.
If we look at the bottom chart, the average is 710.9 and the lowest
channel is about 190. That translates to 710.9/190c= 3.7c
Furthermore, when they quote the average speed they show it with +/-,
e.g. 29.8+/-2.5 cm/ns. This gives the impression that the
speeds range from 29.8-2.5 to 29.8+2.5 cm/ns. In reality that
+/- is not a range but an estimated error of the average speed
calculation – the range in speeds is much broader.
Let’s be clear. If the average speed of many particles is c,
and some are less than c, this requires that others must be moving
faster than c. There’s no way around this, unless we redefine
what an ‘average’ is.
So why do they highlight the average speed and not maximum and minimum
speeds? Hard to know, but perhaps because a maximum >c
is considered impossible and therefore shouldn’t be reported on.
Time dilation or Length contraction?
Returning to the Frisch & Smith video, there is something else of
interest. In the video, time dilation calculations are done to
explain why muons coming down through the atmosphere are decaying slowly
and why they outlive stationary muons at ground level. But as
pointed out earlier, from the view of the muons coming down, they are
motionless and the ground-muons are moving up at exactly the same
speed. So why not do the calculations the other way around?
Toward the end (from 31:30) the presenters raise this
question. Their explanation is that from the view of the
muons coming down, length contraction is occurring and the ground
appears much closer. Therefore they travel a shorter distance and
reach the ground before decaying. This explanation is utterly
inconsistent because the same amount of length contraction must also be
happening from the view of the ground-muons, allowing them to also
travel a shorter distance toward the muons coming down and reach them
before decaying.
In short, they use time dilation from one direction and length
contraction from the other! It’s hard to say whether the
presenters are aware of their inconsistent logic or if they are just
reciting it with a straight face. But it seems they believe
it.
[1] There are also less-common positive-charged muons of equal mass,
making them “heavy positrons”.
[2] Calculation: 0.5 * 3x108 * 2x10-6 = 300m
[3] T.M. Helliwell, Special Relativity, Chapter 6.2, option 4
[4] http://web.mit.edu/lululiu/Public/pixx/not-pixx/muons.pdf
|


