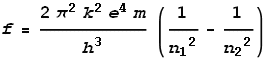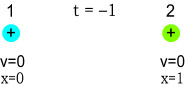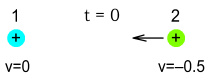Matter-Energy Conversion

One of the more interesting tricks our universe is able to conjure is the conversion between matter and energy. Whenever you see a flash of light, the object that emitted it loses a small fraction of its mass, becoming slightly lighter. Likewise when an object absorbs light it gains a tiny amount of mass.

This phenomenon is known as matter-energy conversion. It operates at all levels, from the movement of electrons between shells to the fusion and splitting of protons and neutrons within a nucleus. That such a thing could happen at all is amazing because, on the face of it, electromagnetic waves, such as visible light, appear to have nothing in common with the hard substances everyday objects are composed of.

E=mc ² ?

The extent of conversion between matter and energy is governed by the famous relativistic energy equation E=mc². Essentially this equation tells us that the total amount of energy available in a given amount of mass (if the mass could be fully converted to energy) is determined by multiplying mass by the speed of light squared.

This formula can be derived by using an application of Special Relativity (SR) formulas. I’ll leave out the derivation as you can see it at a number of sites such as here [1].

At this point some alarms may sound. In the early chapters of this book I highlighted a multitude of problems inherent in SR theory. If these objections are true does that mean this energy equation is faulty? Let’s put that question aside for now and investigate the process of conversion.

Bohr’s Hydrogen atom

In an earlier chapter on atomic orbits we looked at the Bohr model of the hydrogen atom. In this model, electrons orbit only at fixed distances from the nucleus and are able to jump between orbits. When an electron jumps from a high to a low orbit (i.e. closer to the nucleus) it emits a photon of specific frequency.

The matter-energy conversion principle tells us that, when this photon is emitted, the mass of the atom must decrease because energy has been created. This raises an interesting question. If its mass decreased, which part of the atom lost it?

The only parts of the hydrogen atom are the proton and electron. Does the proton or the electron lose? Since the electron is the object that is moving between shells (in fixed orbits), presumably it is this that loses mass. Alas, this creates a dilemma.

Bohr has an equation that accurately predicts the frequencies based upon which shells the electron moved between. It is in this form:

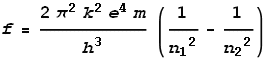
Where f is frequency, k is coulomb’s constant, e is electron charge, h is Planck’s constant and n₁ and n₂ are integer values for the shells being moved between.

Note the m in this equation which represents electron mass. If that mass were changing then the calculated frequency would be different. Considering that this equation predicts the frequencies correctly however, this indicates its mass cannot be changing. After all, a decrease in mass would surely change its orbital behaviour.

So if the electron is not losing mass, what about the proton? Seeing as it is far heavier, the proton could certainly afford to lose quite a bit. As far as we can tell however, the proton is not involved in the electron’s transition between shells. So it seems odd that the proton should lose anything.

Yet the fact that energy-releasing chemical and nuclear reactions cause materials to become lighter is undeniable. How could this be? We need to look deeper into the possible mechanisms involved.

Understanding mass

To determine how the mass loss could be occurring, consider the question:

What is mass?

Okay that’s a tough one. So let’s rephrase:

How do we measure mass?

That’s easier. Basically there are two ways: one is by gravity and the other by inertia. Using gravity to measure mass involves putting a mass on a scale, like a spring scale, and measuring the force based on the stretch of its spring. Using inertia involves applying a known force to a mass and measuring its rate of acceleration.

In practical terms gravity is the easier option. The problem with gravity however is that the measurement varies with the gravitational field. For example, a spring scale would show a one-sixth mass while on the Moon, and zero while aboard an orbiting satellite. Inertia-based measurements don’t have this problem and will give the same result everywhere. So let’s focus on inertia-based measurements and leave the gravity aspects for later.

Now for a very important question:

If something about the process of electrons moving between orbits caused an inertia-based measurement to register a lesser value of mass, would that make the object appear lighter?

Understanding Newton

The motion of objects is governed by Newton’s Laws of Motion. These laws include the principles of momentum and energy conservation. We see these principles in action everywhere; they always work and we have no reason to doubt them.

Another principle is the equilibrium of forces. If you push against an object it always ‘pushes back’ with an equal amount of force in the opposing direction. The average person knows this as “for every action there is an equal and opposite reaction”. To “equal and opposite” we can add “and simultaneous” because the reaction force always pushes back at the same instant.

Or does it?

When you push against something you are not in fact pushing it directly. For example when you use your hand to close a door, your hand does not actually touch the door. Instead the electrons surrounding the atoms in outer layer of your hand come very close to the electrons on the door’s surface. At this point the electron layers push against each other, forcing your hand and the door apart.

The force you feel is really just electrostatic repulsion. The electrons repel each other with an equal amount of force and this gives the “equal and opposite” effect.

Now here’s where it gets interesting. We know that charged particles don’t push each other directly. Instead each particle generates a field, and that field then interacts with other particles. We also know the field travels at a limited speed: light speed. Hence there is a brief delay between when one particle moves and another responds.

A Time and Motion study

To understand the consequences of delayed response let’s study a simple situation involving charged particles. See below.

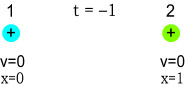
In the above diagram, two positively charged particles are held a fixed distance apart. Let the left-hand and right-hand particles be called particles 1 and 2, and coloured blue and green, respectively. For the sake of simplicity we’ll say they each have a charge of 1 (in arbitrary units), a mass of 1, and are separated by a distance of 1. They are standing still, held in place, and each experience an opposing force of 1 Newtons.

Let the speed of light be 1 unit-distance per second, meaning that it will take 1 second for the field to communicate between particles. The time is now t-minus-one seconds. We will hold the particles in this position for 1 second to allow time for their static fields to reach each other.

Now at t=0 seconds, we release both particles. We give the particle 2 (on the right) a sharp nudge toward the particle 1 so that it is now travelling at 50% the speed of light. See below.

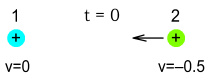
We wish to know how these particles will move and what the effect of the field delay will have. To begin with however, let’s take the standard case where we assume that light moves at infinite speed and interactions are immediate.

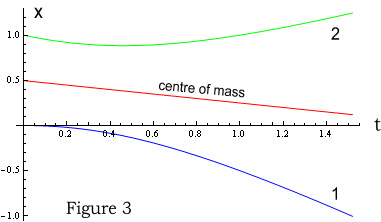
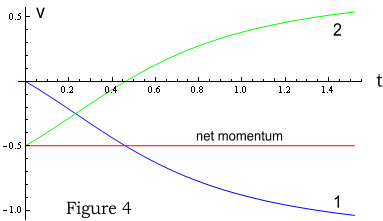
The above charts shows position and velocity of particles 1 and 2 over a 1.5 second period. Figure 3 shows their positions (blue and green lines), with the red line being their centre of mass. Figure 4 shows velocities with the red line representing total momentum. As expected, the centre of mass moves in a straight line and momentum is conserved; remaining constant throughout.

Next we’ll set light’s speed at 1 unit-per-second.

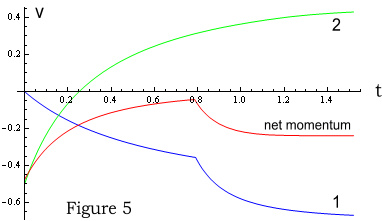
Figure 5 shows the velocity of particles 1 and 2 and total momentum (same colour scheme). For the first 0.8 seconds, particle 1 (blue) follows the same path as before. Suddenly it is hit with the impact of particle 2’s field moving at 0.5c to the left, which increases 1’s acceleration.

Particle 2 (green) is different from the previous scenario. It immediately feels a large resistance due to its movement into particle 1’s existing field. At 1.2 seconds, particle 2 feels a decrease in force from particle 1’s field, due to particle 1’s initial movement to the left. Particle 2’s acceleration then decreases slightly (although difficult to see in the chart).

What’s more important however is the momentum (red line). As can be seen it is not a constant and has not been preserved.

The above chart (figure 5) was made using the VDCL (Velocity Dependent Coulomb’s Law). For comparison, let’s repeat the above using standard Coulomb’s Law.

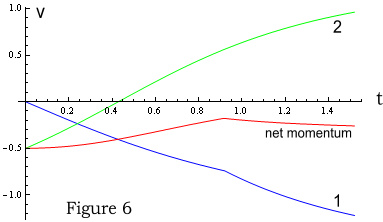
In Figure 6 particle 1 (blue) behaves very similar to the infinite-speed-of-light situation. Then at 0.92 seconds it is hit by an increase in field from particle 2. Particle 2 (green) immediately feels an increase in force from particle 1, due to being closer; although the force does not increase as much as with the VDCL case. Then at 1.36 seconds it experiences a slight drop-off in force due to particle 1’s movement (although difficult to see in the chart).

The important thing to note however is that momentum (red line) is still not preserved, even with standard Coulomb’s Law. Although it is not as distorted as the VDCL case.

Playing croquet

Let’s look at how this might translate into a loss of mass. Imagine you are holding a croquet mallet (hammer) and are about to hit a ball. See below.

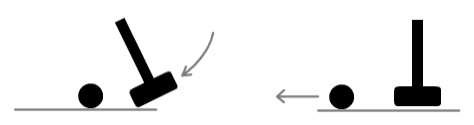
In the left frame the mallet is approaching a stationary ball. In the right frame the mallet has hit the ball which is now speeding away. If we know the mass of the mallet and velocities of the objects before and after, we can determine the mass of the ball using momentum conservation laws.

Now let’s say there are a row of similar balls and you are striking them one at a time, applying the same amount of force to the mallet each time. As you do so, you observe that each ball moves away at the same speed. You then strike a ball and notice that it moves away at a higher speed.

Your first thought would be that this ball must be lighter than the others. This conclusion would be based on your familiarity with momentum laws. But what if the ball actually had the same mass as the others and yet somehow pushed harder against the mallet? This would cause it to move away more quickly and give the impression that it was lighter. How could that happen?

Compare the motion between figures 4 and 5 above. In figure 5, notice that when particle 2 (green) initially moved rapidly to the left it received a strong push-back from the field of particle 1 (blue). This caused particle 2 to be pushed more quickly to the right than it did in figure 4. Initially particle 1 saw none of this motion and, by the time it did, it was further away and thus had less of a response. The net result was that particle 2 moved more quickly away from particle 1, as though it were lighter.

The key here is acceleration. Particle 2 felt a sudden increase in opposing force because it increased its velocity toward particle 1. Had particle 2 approached 1 from a great distance with steady velocity, 1 and 2 would experience equal and opposite forces.

Electron orbits

Let’s now look at how this might affect atoms. When an electron drops to a lower orbit it moves closer to the nucleus and feels a greater attractive force. Much like planets close to the Sun, it would need to orbit faster in order to maintain stability.

But not only will velocity increase, so too will its acceleration when viewed along one direction. The effects of this can be seen in the following sequence of diagrams.

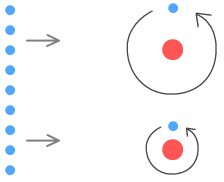
Above are two hydrogen atoms with their electrons in different orbits. The top atom has a high orbit and the bottom atom a low orbit. To the left is a wall of electrons which represent the outer skin of an approaching object. At this distance the wall is too far away to have much effect on the atoms.

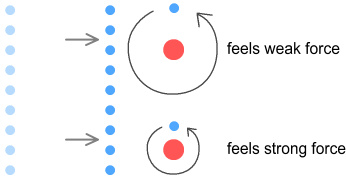
Now the wall (above) is at distance where the particles interact with it. The high-orbit electron moves and accelerates slowly into the field of the approaching wall. As a result if feels a weak opposing force. The low-orbit electron moves and accelerates quickly into the field of the approaching wall. As a result it feels a strong opposing force.

The end result is that the low orbit atom moves more quickly away from the object than the high-orbit atom.

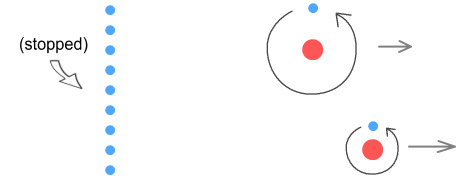
This gives the impression that the low-orbit atom weighs less than the high-orbit atom, whereas in reality they weigh the same.

Self propulsion?

As can be seen from the above demonstrations, which were derived from computer simulations by the way, the limited speed of light causes momentum and centre of mass to not be perfectly preserved. An interesting application arises from this.

It should be theoretically possible to cause an object to shift its centre of mass without pushing against an external object. This would involve electrically charged components within the object being accelerated against each other in an appropriate manner. Done correctly, this would cause a net increment of velocity in a given direction. If this process were repeated continuously it would lead to any desired end velocity, even greater than light speed, without needing to eject a propellant.

To see how this might work in reality, see this supplemental chapter:

Ideas for Propellantless Propulsion (<-- click to read)

Other considerations

The above conjectures are incomplete as they don’t provide equations to predict the extent of apparent mass loss. We also need to consider how this mass loss may work in the case of gravity measurements and how the joining of protons and neutrons could cause changes in mass.

Conclusions

Newton’s laws of motion are based on an assumption that opposing forces between objects operate simultaneously. Under normal situations this is a perfectly reasonable assumption. When two objects impact each other, i.e. ‘touch’, the distance between them is so small, and the speed of light so fast, that response time could be considered instantaneous.

But this is not always the case. The finite speed of electric fields means that under situations of high acceleration the motion of charged particles does not follow the expected Newtonian path.

When electrons move into lower orbits they move and accelerate faster. This causes them to give a higher degree of repulsion against the field of a second atom. This in turn can make the first atom appear to have lost mass, when in fact its mass has not changed.

[1] See https://en.wikipedia.org/wiki/Relativistic_mechanics#Kinetic_energy which gives the derivation for relativistic kinetic energy. Click [show] for the intermediate steps.