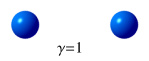Problems with Length Contraction

Special Relativity (SR) tells us that moving objects should shorten in length along their direction of travel. E.g. assume that an electron has a spherical shape. When at rest relative to an observer, the electron appears spherical as expected. Then as the electron moves away from the observer, it appears to shorten. And as it approaches the speed of light it will appear to flatten out like a discus, approaching zero length as the speed nears that of light.

This is called Length Contraction (LC). The amount of contraction will be in accordance with the Lorenz Transform (LT), represented by the symbol γ. The below diagram gives an idea of what might happen to the electron at different speeds.

The speedy rocket ship

LC is normally not described using single particles but with larger objects such as a high-speed rocket. The claim is that when the rocket is still it has a certain length, and when the rocket moves at 0.87c it shrinks to half that length (relative to an observer).

Given that a rocket is not a single particle but made of many particles (atoms) the above claim appears to raise an anomaly. What it is saying is that not only do the atoms shrink but the space between atoms also shrinks, resulting in a shorter rocket. Somehow the LT has been applied to the space between the atoms. But how can empty space shrink, especially when space is not a physical object and therefore cannot be considered to be moving?

The reason for this actually has to do with another aspect of SR called repositioning, which will be discussed later. For now though we can consider the particles making up the rocket (atoms) move in unison and thus form a ‘super particle’ to which we apply the LT. So let’s just take that as being the case and proceed from here.

Problems

LC seems easy to picture when a single particle is involved. However a problem emerges when several moving particles are considered. Let’s say we have two electrons a fixed distance apart and initially at rest. They might look like this:

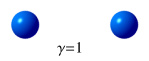
Now the electrons begin to accelerate at an identical rate until they reach a speed of 0.87c. At this speed the LT tells us that they should shrink to about half their length, i.e. γ=2. Here’s a question: according to an external observer, which of the below diagrams (A or B) now best represents the electrons?

The correct answer must be B. If the distance from the front to the back of each electron decreases by half, then the distance between the two electrons must also shrink by half. Both electrons are at rest relative to one another and, like the rocket above, they form a moving ‘super particle’ which also needs to reduce its length by half.

Now let’s say we have a steady stream of equally-spaced electrons in a circular particle accelerator. Initially the electrons are at rest and the situation looks like this:

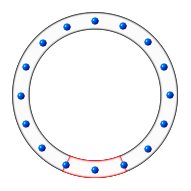
A small tube sits within the accelerator – represented by the red section at the base. The tube has a length that covers the spacing of two electrons such that as a new electron enters, an old one exits, and a third electron sits at the mid point. When the electrons are at rest the tube situation looks like this (for convenience, the tube is shown flattened out):

Now let’s power up the accelerator; applying equal acceleration to all the electrons until they reach a speed of 0.87c. At this speed the LT predicts that each electron should shrink to about half its length.

Question: according to an observer in the rest-frame of the laboratory, which of the following diagrams: A, B or C, best represents the new situation inside the tube?

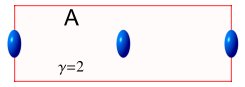
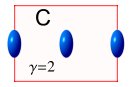
(A) shows the electrons shrinking but their spacing staying the same.
(B) shows both electrons and spacing shrinking but the tube staying the same.
(C) shows the electrons, spacing and tube all shrinking.

(A) cannot be correct because the electrons are all moving together as a ‘super particle’ so the distance from the front to the end of this particle must also shrink.

(B) is correct as far as electrons go, but incorrect as regarding the tube because electrons must line up with the each end of the tube.

(C) satisfies the requirement for shrinkage of the electrons as a whole while keeping them matching the tube, but is obviously incorrect because it implies that the accelerator must also shrink with the tube.

So the correct answer must be: None of the above.

Since the accelerator is circular and the spacing between each electron is equal, it is not possible for all of the electrons to move closer together without shrinking the accelerator also. Considering that accelerators are not observed to shrink it seems that LC could not possibly occur.

Which direction?

A second question regards the direction of shrinkage. LC tells us that shrinkage should happen along the direction of travel. Consider the following diagram:

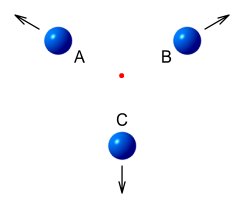
Three balls A, B and C are arranged on the points of an equal-sided triangle and move at equal speeds away from its centre. Suppose we wish to know the contraction of ball C. First let’s consider A and C in isolation. Without having B available as a reference, A and C are moving directly away from each other. So from the point of view of A, ball C should look like this:

Now consider B and C in isolation. Without having A available as a reference, B and C are moving directly away from each other. So from the point of view of B, ball C should look like this:

This is obviously a problem, since ball C cannot be simultaneously shaped like both of the above diagrams.

By how much?

A third question relates to the amount of shrinkage relative to an observer. According to SR all velocities are relative and therefore the amount of shrinkage can be different for different observers.

For example, suppose we have a rod of fixed length and say it is ‘at rest’. Next we take two observers moving length-wise toward the rod but at different velocities. The first observer moves at 0.87c (where γ=2) and the second at 0.94c (where γ=3).

According to the rules of LC, the first observer will see this:

While the second observer sees this:

Again we have a problem because the rod can’t have both these lengths.

Length Contraction and Repositioning

We’ll now get to the nuts and bolts of what is said to be causing LC. Under SR a moving particle will appear to reposition itself according to the formula:

x' = x/γ

Where x is the position the particle would be in if it were not moving, x' is the position it appears to be in once it starts moving, and γ is the LT. Another way of looking at it is: x is the position according to Newtonian (classical) mechanics and x' is the position according to SR [1].

To see how this leads to LC, consider a rod of length L located a distance x from an observer as shown:

Initially the rod is not moving, so SR doesn’t apply and everything appears normal. We now set the rod in motion at 0.87c, which makes γ=2. From the view-point of the observer, the front of the rod repositions itself from x to x/2. Meanwhile the end of the rod repositions to (x+L)/2, which is x/2+L/2. The net result is this:

As can be seen, both the distance to the rod and the rod itself has contracted by a factor of 2. The same applies to all the particles (atoms) within the rod: they reposition themselves and give the impression that the rod overall has shrunk. For this reason ‘relativistic length contraction’ should perhaps more properly be referred to as ‘relativistic repositioning’.

So what about other situations such as when a particle is instead moving toward the observer or moving at an angle?

In the case where a particle (or rod) is moving toward the observer, it is the treated the same as if moving away. That is, it ‘moves’ toward the observer and contracts along its length by the same amount. This is because the LT function contains a v² term, which makes direction unimportant.

In the case where the particle is moving at an angle, i.e. not directly toward or away from an observer, it is a little more complex. Basically though, you need to trace a line along the direction of motion until it crosses a line at right angles that passes through the observer. The length of the first line will be what is used in the calculations. The below diagram explains this. It shows an object’s position according to classical mechanics (without SR), and its new position as will be seen according to SR.

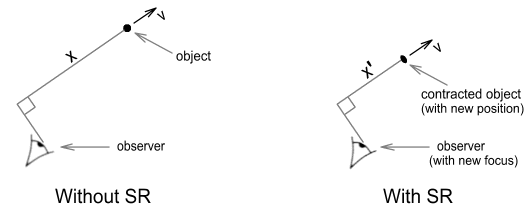
Note that the contraction and repositioning occurs along the direction of travel rather than in the direction of the observer.

Is the Rocket Near or Far?

An interesting story can be told about repositioning.

A rocket starts on Earth and carries an enormous quantity of fuel that allows it to steadily accelerate at 10m/s². At this rate it would reach light speed in just under a year, although we will impose an SR restriction (such as mass-increase) that prevents it from quite reaching that speed.

After 35 days of travelling it has reached 10% of light speed and is 4.5x10¹³m away. After 6 months it is moving at half the speed of light and is 1.2x10¹⁵m away. However due to repositioning it appears closer, at 0.87 times the distance or around 10¹⁵m.

At the 10 month mark it is 87% of light speed and 3.4x10¹⁵m away. Yet due to repositioning, appears to be at half that distance. At the 11.5 month mark the rocket reaches 99.5% of light speed. It is 4.4x10¹⁵m away but appears at only one tenth that distance. We continue in this manner. When the rocket is at 99.99995%c, the actual distance is still around the same, but the perceived is 1/1000^th of that at 4.4x10¹²m. We shift to (1-5x10^-13)c. The perceived distance is now one millionth of the original, at 4.4x10⁹m.

Finally we get to (1-2.5x10^-30)c. At this point the rocket appears to be only 10 metres away and is extremely compressed along its length. So... build a roof over the rocket and capture it!

Now obviously this won’t be possible. The people on the ground will see the rocket 10m above them. Whereas a builder atop the construction would see the rocket 10m above his head, rather than below the roof. Hence the rocket’s apparent location is illusory. But the above story does serve to call into question the LC hypothesis because it requires the roof to be obscured by the rocket.

Length Contraction and Photons

Does LC apply to photons? When light comes from a distant star, photons must start their journey at the star and head directly toward us. Due to the large distance, it takes many years for them to arrive. But why should it?

Since the photons are moving at the speed of light, the distance between them and us should shrink to zero. In other words a photon should be at our eyeballs the instant it is emitted from a star and there should be no delay in them reaching us regardless of how far away their source is.

Clearly this is not the case because there is always a delay in transmission that increases with distance. It appears that length contraction doesn’t apply when dealing with photons. On the face of it there is no logical reason why it shouldn’t apply, and this seems to be a case of conveniently overlooking the rules when they don’t match reality.

Experimental evidence

Now let’s consider what experiments have to say about LC. Measuring LC is no easy task because SR tells us that a moving object’s length immediately returns to normal once it stops. And observing a particle in motion is also difficult as that would normally require bouncing a light beam off the object; and the beam would have trouble reaching a particle moving at near light speeds.

So what do experiments tell us about LC? Here we draw a blank. Several experiments have been either tried or proposed, but they failed to measure that a variation in length occurred [2], [3]. To date no experiment has been able to confirm the existence of LC.

Although there is one test which is said to demonstrate LC in terms of magnetism.  It is discussed in a supplemental chapter:

Magnetic Test of Length Contraction (<-- click to read)

Conclusion

The phenomenon of length contraction is said to be responsible for a number of effects; some of which might be possible from the viewpoint of a single observer, but would be contradictory from the viewpoint of multiple observers.

There may be a semantic issue here. Namely, is length contraction an actual contraction or just an observed contraction as seen from a stationary position? If it is only an observed contraction then it is merely an optical illusion, and is of little importance physics-wise.

Alternately, if length contraction is purported to be an actual contraction, then based on the argument that it is not possible to satisfy both the length and spacing requirements of moving particles relative to a fixed stationary length (see above comments about circular accelerator), and the lack of experimental evidence to the contrary, I submit that length contraction does not occur.

[1] Actually the equation is normally expressed in the form x'=(x₀+vt)/γ where x₀ is the initial position, v is velocity and t is the time taken to get to the current position.
[2] Wood, A.B., Tomlinson, G.A., and Essen, L. 1937. "The Effect of the Fitzgerald-Lorentz Contraction on the Frequency of Longitudinal Vibration of a Rod," Proc. Royal Soc., 158, 606-633.
[3] Renshaw, C. 1999. "Space Interferometry Mission as a Test of Lorentz Length Contraction," Proc. IEEE Aerospace Conf., 4, 15-24.