Analysis of Gravitational Lensing
in Abell 1689
One of the most striking pictures showing gravitational lensing is a gravity cluster known
as Abell 1689 (see below). The gravity from this cluster is able to distort the space
around it to such an extent that the light from objects behind it bends into arcs
surrounding the cluster [1].

Briefly, this picture shows:
(a) a few nearby yellowish galaxies which make up the Abell 1689 cluster.
(b) many distant galaxies, some of which are stretched or curved into arcs
(c) a few nearby stars, distinguished by the cross-hair lens flaring
(d) some other galaxies that aren't stretched.
Let's look at some interesting aspects of this image.
1. Curvature of Arcs
2. Strength of the lens
3. Equivalent optical lens
1. Curvature of Arcs
First look at the distant objects that are skewed into arcs and notice
that those arcs seem to 'orbit' the central area of the cluster. Are those arcs orbiting
multiple points in the cluster or do they orbit just a particular point? To find out we
can draw a set of circles which match the arcs. See below.

In the above image orange circles were drawn to match the arcs, some of which I've marked
with arrows. As can be seen, the alignment of most arcs closely matches the circles
throughout the image.
What's interesting is that the circles appear to be centred on a single point
corresponding to the central galaxy of the cluster (marked in red). Given that the cluster
is made from several galaxies we might expect the curvature to be different at various
points in the image. For example, the arrow that is furthest to the right highlights an
arc that lays almost directly over a small clump of galaxies. We should expect this clump
to have its own set of arcs for background objects closest to it. Instead the arc focuses
on the central galaxy.
To be fair there does appear to be another focal point higher up with at least four arcs
centred on it. See below.

2. Strength of the lens
Next, how strong is this lens? We see a high degree of light-bending.
According to General Relativity this requires a lot of gravity.
Galaxies are massive objects and galaxy clusters even more so. Our own galaxy for example,
the Milky Way, is 200 billion times heavier than our Sun. So clusters of galaxies would be
many times heavier and must therefore have huge gravitational fields, right?
Not quite. As large as our galaxy is, its gravitational field is actually quite weak. So
weak in fact that it takes 200 million years for our Sun to complete an orbit. The reason
is that distances between stars are quite large, and distance rapidly reduces gravity by
the inverse square. Based on how our Sun moves through the galaxy we can estimate it
experiences a gravitational pull of 2x10-7 m/s2. That's 50 million
times weaker than Earth's surface gravity!
So here's the problem. We know from observation that the strength of gravity near our Sun
is only sufficient to bend light by a barely perceptible amount. Yet the Abell 1689
cluster, whose gravity must be far weaker, is able to bend light by an enormous degree.
If Abell 1689 did have the amount of gravity necessary to bend light like this, its forces
would rapidly pull the cluster together. But Abell couldn't have such gravity because, due
to increased distances, the gravity outside a galaxy is far weaker again than the already
weak gravity within it. That would explain why the cluster barely moves.
3. Equivalent optical lens
Finally we need to look at how this strange lensing effect might occur. If
gravitational lensing is similar to optical lensing, what sort of optical lens could
stretch points of light into curved arcs? A standard convex lens, like a magnifying glass,
won't do it. But there is a type of lens that will - a ball lens. A ball lens is basically
a solid sphere of glass or other transparent material. It's a strong version of a convex
lens that works in any direction.

The above picture on the left shows a ball lens held close to some news print. The one on
the right shows it being held to a distant scene. As can be seen the ball acts similar to
a magnifying glass - enlarging nearby objects and inverting distant ones. However there
are some differences, namely that the steep edges cause the image to go 'crazy' at the
outside. This can be seen below.

Here the ball is being held in front of an array of dots. As can be seen, dots along the
outside edges are stretched into short arcs. This is just like the objects behind the
Abell cluster. But unlike the cluster, the curved dots in the above picture lie only along
the edges of the ball. Outside of that they end abruptly. Behind the Abell cluster
however, the arcing continues all the way to the image frame.
Clearly, a ball lens couldn't do this. So what could? In theory it's possible to form a
lens for any desired effect. To speculate let's have a look at something called a Fresnel
lens. A Fresnel lens is one made by taking a regular lens and compressing it into
segments, such as shown below.
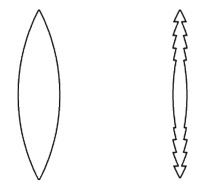
On the left is a regular convex lens. On the right is the Fresnel
version of it. Only the slanted surface portions are preserved because these are what
cause magnification. Interior portions are 'discarded' [2].
The above lens however will only work like a regular magnifier. We want something like a
ball lens. This could be achieved with the below formation.
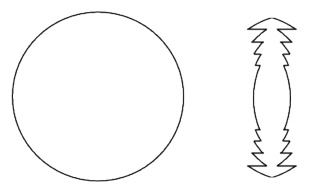
On the left is our ball lens. On the right is the Fresnel version of it.
In theory this should function like the ball and cause arcs to appear along the edges. But
what if we want them throughout?
We know that it's the edges of the ball that cause the stretching effect. So it should be
possible to achieve this effect throughout the image by using ball-edges throughout the
lens, such as shown below.
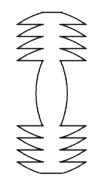
In theory the above lens, consisting of a series of ball-edges arranged in
concentric rings, should stretch a background of point-lights into short arcs like those
shown in the photographs.
While this lens might work however, it would only work in one direction, meaning that the
effect would only be seen by those on the direct opposite side. It goes without saying
that it's difficult to imagine how the gravity of Abell could have arranged a neat set of
strongly curved-space Fresnel segments that nicely line up with Earth.
Setting aside this multi-segment requirement, there's a further problem. In the above
image showing the array of dots stretched into arcs; this only works when the lens is held
close to the dots. If you move the dots further away than the width of the ball - about
double its focal length - the whole image simply inverts and no stretching is visible. The
galaxies behind Abell are many times further away than the width of the cluster. They are
at what we call 'optical infinity'. Therefore it is difficult to see how the lensing
effect could do anything other than invert them.
Conclusions
What can we say about the Abell cluster and its surrounding objects? It
curves light around its central galaxy but not around its surrounding galaxies. It bends
light in a manner that almost no optical lens could achieve. And does so to a degree
requiring gravity immensely greater than any galaxy cluster could possess.
Could this be an altered image? Perhaps an over-zealous attempt to prove the effects of
gravitational lensing? It is difficult to say without independent observation/confirmation
of the same image. But until this, or until there can be found explanations for the above
anomalies, we should consider this a possibility.
[1] Regular size image here:
http://en.wikipedia.org/wiki/File:Abell.lensing.arp.750pix.jpg
Click on it to enlarge. Super-sized version here:
http://imgsrc.hubblesite.org/hu/db/images/hs-2003-01-a-print.jpg
[2] Actually, Fresnel lenses are normally flat on one side. The
lenses shown here will probably need some adjustment to make them work.
|