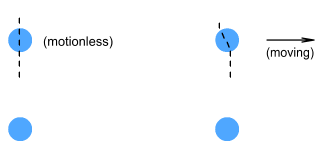Superconductivity

Superconductivity is a phenomenon in which some materials lose all electrical resistance at very low temperatures. For example if Lead is gradually cooled its resistance steadily decreases (this is common for most conductors). But if cooled below 7.2 degrees Kelvin its resistance suddenly drops to zero. In this state a ring made of lead is able to conduct a current that cycles for years (creating magnetic fields) without any observed decay.

A current moving forever in a loop is a seeming impossibility. It breaks the rules of electrical resistance, physical friction and thermodynamics; all of which would predict some sort of energy loss. After all, even if the loop were made of the best non-superconducting conductors available the current would rapidly dissipate.

Understanding resistance

To gain an understanding how superconductivity might be happening we first need to look at how conventional electrical resistance occurs. According to accepted theory, resistance to current flow occurs because electrons keep ‘bumping into’ atoms as they flow through a conductor. Thermal activity also plays a role. As a substance increases in temperature its atoms move more vigorously. This movement increases an electron’s resistance to flow because it increases the number of collisions. Conversely as a substance cools the number of collisions, and hence the resistance, decreases.

This theory appears quite sound. But it should be added that it is not necessary for the electrons to actually collide with atoms; electrons merely need to pass nearby atoms in order to experience a multitude of interfering electrical forces.

The BCS Theory of Superconductivity

So how does superconductivity work? The standard explanation is ‘BCS theory’.

BCS states that electrons move through crystalline lattices in pairs due to vibrations in the lattice and the spacing of electrons within it. Because of the Pauli Exclusion Principle these pairs operate together at a low level of energy that inhibits the kind of collisions that lead to resistance.

There is more to BCS than this of course. The above is heavily summarized and it’s recommended that the interested reader pursue a more detailed description [1].

An alternative explanation of Superconductivity

Is BCS correct? It is difficult to say, especially as it involves quantum mechanics explanations that lay outside the boundaries of our real-world (and common sense) experience. So I’d like to present an easier-to-swallow alternative that fits within classical mechanics.

Firstly we note that superconductors are crystalline compounds whose lattices form long straight paths that electrons can move along. At low temperatures the vibrations of these lattices would reduce to a point where there are unobstructed straight-line paths between rows of atoms.

So far so good. But could a straight-line path lead to a no-collision, and hence zero-resistance situation? It is tempting to think so. Unfortunately there are problems with this idea:

1. Even if electrons didn’t collide with nearby atoms, those atoms would be surrounded by electric fields that would have a retarding effect on passing electrons.

2. Since superconducting loops are curved there cannot be any overall straight path for the electrons to travel along. The electrons must collide with atoms along the curved sections.

Thus it is impossible for electrons to move through a compound without experiencing a retarding force, even at absolute zero temperatures. This retarding force should bring the electrons to a halt. Yet the electrons don’t slow down; they continue at a constant speed. The only way this is possible is that the electrons are receiving a counter force in their forward direction.

What could that force be?

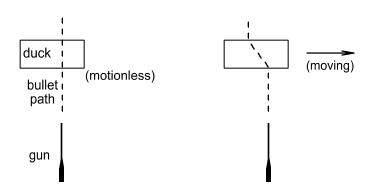
The Duck Hunter

Imagine there lived a duck hunter. This hunter was not very successful because, for some reason, he only shot ducks that flew directly overhead. The ducks flew at varying speeds, some even hovering occasionally, and as they passed he would fire a bullet.

The below diagram represents two successful shots. For simplicity the ducks are drawn shaped like bricks.

The duck in the left frame is hovering, i.e. moving with zero velocity, and the duck on the right is flying with a constant velocity toward the right. As the bullets pass through they exert force on the ducks. In what direction will these forces be?

For the duck that is hovering, the bullet exits directly above where it enters. Therefore the force (F) will be vertical and directly away from the hunter. For the duck that is moving however the entry and exit wounds don’t line up. Since the duck is moving to the right, the bullet moves through the duck on an angle and exits to the left of its entry point. Given that the bullet’s movement is on an angle, its force on the duck should likewise be on that angle, as shown below. This seems odd at first because the bullet is still moving vertically relative to the hunter.

Shooting at Electrons

What does this have to do with electrons? In the preceding chapters electric fields were likened to bullets. Tiny electric field ‘bullets’ emerge from all sides of an electron and travel in straight lines. When these bullets strike another electron they exert a force in the direction of their motion.

Now consider these electron interactions:

The frame on the left shows two electrons standing motionless above and below each other. The frame on the right shows the bottom electron motionless and the top electron moving to the right at a constant velocity. What will the force be on the top electrons?

Referring to our duck analogy, the top electrons are the ducks, the bottom electrons are the hunter, and the electric fields coming from them are his bullets. The field flows through the top-left electron vertically and yields a force directly away from the bottom-left electron. No surprises there. But what about the top-right electron?

Since that electron is moving to the right it seems logical to suggest that the electric field ‘bullets’ from the bottom electron must, like the duck, also move through on an angle (as shown above) and thus cause the net force to be on that same angle:

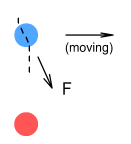
Now suppose a proton was doing the ‘shooting’ instead. What would the direction of force be on an electron moving overhead? Again we expect the field to flow through it on an angle however, due to this being an opposite charge, it seems logical that the force should be in the opposite direction:

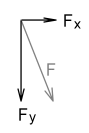
Using vector representation we can split this force into its x and y components:

Notice that most of the force is still in the vertical direction (y axis) but there is now a small force component in the horizontal direction (x axis).

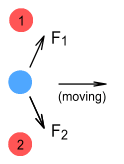
The proton tunnel

Expanding on the above, imagine there are two protons, above and below each other, and the electron is at their midpoint moving horizontally to the right:

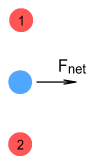
The two protons will exert a diagonal force on the electron; however the forces will not be directly opposite. In the above diagram F₁ and F₂ are the forces from protons 1 and 2 respectively. Taking the vector components of each force we notice that the vertical components cancel, but not the horizontal forces because they’re in the same direction. The net result is this:

The horizontal forces combine yielding a net force to the right.

Finally, imagine there are a row of neatly spaced protons, directly above and below each other forming a tunnel. An electron enters that tunnel on the left:

As it passes between the first pair of protons, the electron will receive a net force to the right. This will propel it to the next pair of protons, whereupon it will receive another force to the right... propelling it to the next pair… and so on, and so forth.

The proton tunnel represents a crystalline lattice found within superconductors. Providing that the electrons continue moving they will continue to experience a forward force. If this force is greater than the force of electrical resistance, the electrons will continue moving in a loop forever, creating the phenomenon we call superconductivity.

Conclusion

It is possible to explain superconductivity within the boundaries of classical mechanics by considering that electrons moving at right-angles to protons receive a small force in their direction of motion due to field lines passing though charged particles at an angle.


[1] E.g. http://hyperphysics.phy-astr.gsu.edu/Hbase/Solids/bcs.html