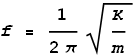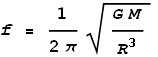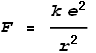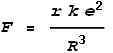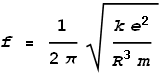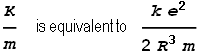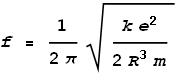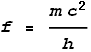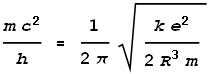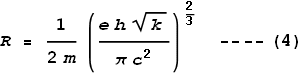Determining the Electron Structure

Following the discussion in the preceding chapter about the interaction between electrons and positrons in producing gamma rays, some interesting clues emerge about the structure of an electron.

What does an electron look like; what is its shape and, more importantly, how big is it? Questions of this nature rarely have any place in modern physics. When it comes to electrons, we know of their mass and charge... and that’s it [1]. As far as structure goes they are considered to have none. They exist as point charges with a size of zero.

To say that an object has mass and no size is to say that it has infinite density. Perhaps this is true for an electron, but infinites of any quality rarely have a place in the real world. It is thus more realistic to suggest that an electron does have a non-zero size, even though it be exceedingly small and irrelevant in most considerations.

The purpose of this discussion then will be to determine what an electron’s shape and size might be. To begin with we’ll assume that it’s spherical. The reason for this assumption is that a sphere is the ‘purest’ of 3D shapes and makes an electron’s field appear identical in all directions. Now the hard part is finding its radius.

The classical electron radius

Before going further some points need to be made about something called the ‘classical electron radius’. This is a calculated radius based on an assumption that the mass-energy potential of an electron is fully contained within a certain radius [2]. It has a value of 2.82x10^-15 m.

That’s certainly small. Now compare this with the measured radius of a proton, which is 1.11x10^-15 m [3]. According to this an electron has a radius 2.5 times larger than a proton. Given that a proton is around 2000 heavier however, it’s difficult to know if we should take this ‘classical radius’ seriously.

A more realistic approach would be to take the ratio of proton/electron mass, then divide the proton’s radius by the cube root of this number (because mass increases according to the cube of radius). This ratio, 1836, would set the electron’s radius at approximately 12 times smaller than a proton: at 9.1x10^-17 m.

If a proton and electron were made of similar material and the proton had uniform density, this would be close to the correct value. Alas a proton is believed to consist of other particles called quarks (to be discussed in a later chapter). If these quarks occupy only a small volume within a proton, this would greatly lower its density and the electron’s radius would calculate to be far smaller again, perhaps by an additional factor of 10 or 100.

With this in mind, let’s now see if the positron-electron interaction can reveal better information.

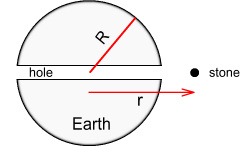
Falling through the Earth

Imagine you bored a hole through the Earth – straight down through its centre and out the other side. Next you dropped a stone at the entrance. The stone would fall rapidly at first, gaining in speed until it reached terminal velocity. It would then continue toward the Earth’s centre and past it. Once beyond the mid-point it would decelerate as it neared the other side. The stone would then oscillate several times until it came to rest at the Earth’s centre.

Let’s assume instead that there was no air and the stone was able to move all the way from one side of the Earth to the other and back again, much like a pendulum. What would be its precise motion of oscillation, and how long would it take for a full ‘swing’?

At first glance this looks like a difficult problem to solve because the force function of gravity is inversely proportional to square of distance. And beneath the Earth’s surface it would become even more complex. Solving the force function requires some tricky calculus. But as luck would have it the solution is surprisingly simple.

Above the surface the force follows the familiar Newtonian function:

$F = \frac{G M m}{r^2}\text{ ----}(1)$

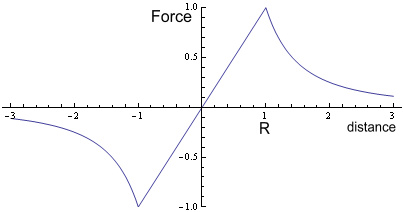
Where M is mass of Earth, m is mass of an object (the stone in this case) and r is distance from the centre. Below the surface the force follows a linear function:

$F = \frac{r G M m}{R^3}\text{ ----}(2)$

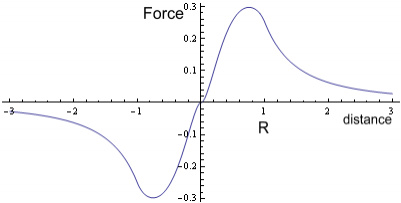
Where R is the radius of the Earth. If we were to plot this it would show (setting, G=M=m=R = 1, and including force direction):

gravitational force through the earth

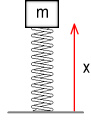
A simple spring oscillator

To understand what this means we’ll look at a simple spring oscillator.

spring oscillator

Above we see an object with mass m attached to a spring. The spring has a stiffness of K meaning that, e.g. if K was 5 N/m then every 1 metre of stretch would require 5 Newtons of force. Assuming we are in a zero-gravity environment and the mass could move below the baseline, what function would describe the position of the object with respect to time?

The problem we are trying to solve is:

Force = mass * acceleration, which is:

$-x(t) K = m x\text{''}(t)\text{ ----}(3)$

Where x(t) is the height of the object at any time t and x’’(t) is its double derivative – i.e. its acceleration.

The solution to this is well known:

$x(t) = A \cos \left(\sqrt{K/m}t\right)$

Where A is the initial height and we assume the object to be initially motionless. In other words, the object oscillates as a pure sine wave. The frequency of oscillation will be:

$f = \frac{1}{2 \pi }\sqrt{\frac{K}{m}}$

And the period of oscillation will be the reciprocal: T=1/f.

Now let’s apply this to the stone moving through the Earth. We can rewrite (3) as:

Acceleration = -K/m * distance

Inside the Earth acceleration is (from equation (2)):

Acceleration = F/m = -G M/R³ * distance

(a minus sign was inserted to make direction consistent). Here we see that

K/m is equivalent to G M/R³

Therefore frequency will be:

$f = \frac{1}{2 \pi }\sqrt{\frac{G M}{R^3}}$

Inserting values for G, M and R, and taking the reciprocal we get a period of 5060 seconds, or 1 hour 24 minutes. Thus it will take just under one and a half hours for the stone to return to its starting point.

Falling through an electron

What does any of this have to do with electron-positron interactions? Well, gravity is a good analogy to the electric force because it varies in inverse proportion to distance. If we think of an electron as spherical and assume that its charge is uniformly distributed then its force function (exerted on a positron) would be very similar to Earth’s gravitational field, namely:

Outside the electron the force would follow the familiar Coulomb function:

$F = \frac{k e^2}{r^2}$

Where k is Coulomb’s constant, e is an electron’s charge and r is distance from centre. Inside the electron the force would follow a linear function:

$F = \frac{r k e^2}{R^3}$

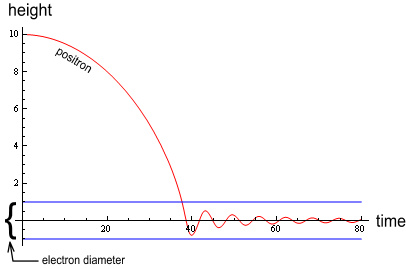
Where R is the electron’s radius. If the positron were to oscillate only within the electron this would produce a sine-wave motion. Does it oscillate within the electron? The below chart shows a simulation of the event:

positron oscillation through electron, with electron held fixed

In this diagram a positron (red line) falls from a height equal to 10 electron radii. As can be seen the VDCL (Velocity Dependent Coulombs Law) causes much dampening during the initial fall, causing the oscillations to lie fully within the electron (blue lines). Thus we can calculate the motion of oscillation based on the forces within the electron and ignore the force function outside it.

Relating this back to our spring oscillator, we see that:

$\frac{K}{m}\text{ is equivalent to }\frac{k e^2}{R^3 m}$

Meaning that frequency of oscillation will be:

$f = \frac{1}{2 \pi }\sqrt{\frac{k e^2}{R^3 m}}$

Solving the two body problem

At this point it would be tempting to plug values in and calculate a value of R that corresponded to the observed frequency. However there’s something else that needs to be taken into account; namely that is we are not dealing with a stone falling through the Earth. Rather, we are dealing with two earth’s falling through each other, or in this case, an electron and positron oscillating through each other.

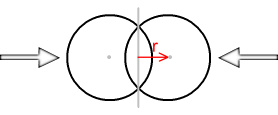
Determining the force function for two spheres is going to be more complicated. As it happens, the force function will be same as the normal Coulomb force when the spheres are outside each other, i.e. not overlapping. When they are overlapping the function becomes very complex but here’s what it looks like:

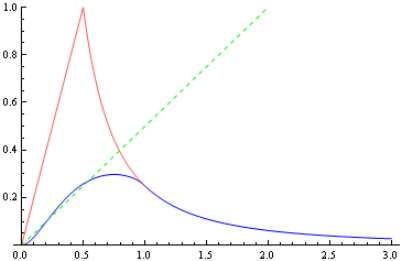
The x-axis represents the distance from the mid-point of the two spheres because this is the point that the spheres will be mirrored on. As can be seen the force function is ‘rounder’ than the single sphere situation and is not a straight line. Here is a comparison between the two functions:

The blue line is the two-sphere force function, red is the single sphere situation (shown for comparison), and the green dotted line represents half the gradient of the red line. As can be seen the force function for when the sphere’s overlap closely approximates half the strength of the single sphere situation. Thus we can relate this back to our simple spring oscillator and find that:

$\frac{K}{m}\text{ is equivalent to }\frac{k e^2}{2 R^3 m}$

Meaning that frequency of oscillation will be:

$f = \frac{1}{2 \pi }\sqrt{\frac{k e^2}{2 R^3 m}}$

We know that this frequency must correspond to the one calculated from quantum mechanical and relativistic energy equations, namely:

Meaning that:

$f = \frac{m c^2}{h}$

Where h is Planck’s constant. Next we match these two frequencies together:

$\frac{m c^2}{h} = \frac{1}{2 \pi }\sqrt{\frac{k e^2}{2 R^3 m}}$

Isolating the radius term we get:

$R = \frac{1}{2 m}\left(\frac{e h \sqrt{k}}{\pi c^2}\right)^{\frac{2}{3}}\text{ ----}(4)$

Substituting the standard values for e, h, k and c, we find that radius of an electron R comes to: 5.94x10^-14 m.

Discussion

This is disappointing. We wanted a radius at least a hundred or so times smaller than a proton. Instead we calculate one fifty times larger. It’s hard to believe that this number reflects the true electron radius.

On the other hand it is not terribly far out. If we were to randomly arrange the universal constants e, h, k and c, we would most likely end up with numbers that are far too large, or even too small, to represent an electron’s radius. The number we have, 6x10^-14 m, is within the ballpark of the atomic neighbourhood, representing 1000^th the radius of a hydrogen atom.

Therefore, rather than disregard the above hypotheses, is seems appropriate to explore some possibilities.

Is the frequency correct?

The first possibility is a question of frequency. The frequency of gamma radiation arising from electron-positron annihilation is quoted as 1.24x10²⁰ Hz. But this is not a measurement, only a calculation based on the physical constants; namely frequency = mc²/h. It is not possible to measure frequencies this high, e.g. by electronic counting, because we have no instrument that can keep up with the oscillation rate.

When we made the above calculations of electron radius we were assuming that the quoted frequency value was correct. But what if it was higher? For example a frequency of 10²³ Hz would make the calculated radius 100 times smaller, or 1/20^th the radius of a proton. And a frequency of 10²⁶ Hz would set the radius 10000 times smaller, or 1/2000^th that of a proton. Could the frequency be that high?

A radio antenna comparison

Some interesting analogies can be drawn between the high frequencies of gamma rays and the low frequencies of radio transmission. We know that a radio receiver’s antenna is most effective when its length matches half the wavelength of the transmission frequency. For example a Wi-Fi wireless computer network operating on 2.4 GHz uses antennas around 6 cm in length because the wavelength of that frequency is 12.5 cm.

That quoted gamma ray frequency of 1.24x10²⁰ Hz corresponds to a wavelength of 2.4x10^-12 m. This is around 2000 times larger than a proton. If protons behaved like radio antennas, we would not expect this wavelength to have much effect on a proton. Yet we know that gamma rays do interact with atomic nuclei because the nuclei absorb them. To be properly absorbed by a proton the frequency would need to be 1000 times larger: around 10²³ Hz. To be absorbed by an electron the frequency may need to be 1000 times larger again; at 10²⁶ Hz.

Admittedly this doesn’t prove the frequency is this high because frequencies can still be absorbed even when the antenna is not of the ideal length. Nonetheless it is interesting that the wavelength-matching requirement at the atomic-distance scale requires frequencies in the range we are seeking.

Energy/frequency conversion formula

When determining the gamma ray frequency, we did so from its energy using the formula E=hf; where E is energy, f is frequency and h is Planck’s constant. This formula is used to calculate the energy of a photon based on frequency, especially photons created when electrons transit between atomic shells.

It is undoubtable that this formula works well when applied to atomic interactions. But does that mean it will also work for every other type of reaction? After all, the mechanisms used to generate photons in the gamma-ray range are very different from those in the visible range. A formula that works well in one situation is not necessarily suited to another.

The E=hf formula implies that we can determine the energy of a photon based on frequency alone. Determining the energy of an electromagnetic wave however requires knowing several things, such as frequency, amplitude and duration. For example, suppose someone asked you to calculate the energy of a laser pulse, but they only told you its frequency. Your first question would likely be: “how long does the pulse last?” Without that information there is no way of calculating the net energy.

So what is the answer?

Unfortunately this lack of information regarding frequency has left us unable to determine the size of an electron. However jumping ahead to the information given in chapters on particle physics and nucleon structure it should be possible to estimate an electron’s diameter based on a proton’s. Without giving away the story in advance, based on this I estimate the radius of an electron to be approximately 10^-16 metres.

Conclusions

The fixed-frequency radiation emitted during electron-positron annihilation indicates that an electron has a spherical structure and its charge is uniformly distributed within.

If an electron and positron were to oscillate through each other they would do so in a sinusoidal motion, generating a short burst of electromagnetic radiation of a specific frequency. If we know this frequency it should be possible to determine an electron’s radius. The quoted frequency of generated gamma radiation however gives a radius that’s too large when compared to a proton, yet not excessive when compared to an atom.

But this frequency may be incorrect because it is a calculated value rather than a measured one. If the frequency were several orders of 10 higher, a more realistic radius would emerge. Alas it is not possible to determine the radius without knowing the correct frequency.

The relationship between energy and frequency given by the equation E=hf does not necessarily hold true for photons being generated by means other than electrons orbiting a nucleus.

[1] Setting aside that strange property called ‘spin’.
[2] By equating E=mc² to E=ke²/r.
[3] http://www.wbabin.net/physics/yue.pdf There are several sources with different values, but they appear to be around 10^-15 m.