A Case for Absolute Velocities

The great philosopher Aristotle held that all bodies have a preferred state of rest, such that once a body was set in motion it would eventually slow to a stop.  Centuries later Galileo and Copernicus overturned this view, stating there is no preferred state of motion and that the velocity of one body only has meaning in relation to another.  That is that all velocity is relative.

Today we refer to this as the Galilean Principle of Relativity (not to be confused with Einstein’s ‘Theory of Relativity’).  It tells us there is nothing special about the motion we experience after all.  The Earth rotates on its axis, which orbits the Sun, which circles within the Milky Way.  And our galaxy then moves in various motions with respect to other galaxies.  We really can’t say anything about our overall state of movement, or even if such a movement has any meaning.

But is that truly the case?

The concept of relative velocities is so well established in scientific thought that to suggest that there may be such a thing as absolute velocities after all must seem like lunacy.  Yet a careful analysis of our physical laws indicates otherwise.  This is not to say that Aristotle was right in his thinking.  No; his absolute velocity was just a velocity relative to Earth’s surface.  What is being discussed here is something far more fundamental that follows unavoidably from the most basic of scientific principles.

The Bar Room Brawl

To illustrate this, suppose you had the ability to freeze time and then walk around and observe things.  In such a situation your world would become completely dark because no light could be generated or reach your eyes.  So we’ll modify the situation slightly and say that a special form of illumination comes into play that lights everything up without disturbing anything.  If you’re familiar with the movie The Matrix, it would be like those scenes where everyone stops and the camera swings around them.

Now suppose you have just used your supernatural abilities to freeze time and had then walked in on a bar-room brawl (a.k.a. a ‘pub fight’).  In this fight, two parties are located at either end of a room behind upturned tables and are hurling projectiles, such as bottles, cans and glasses, at each other.

Several projectiles are in the air at once, but since time is frozen, it’s not clear which direction they are moving.  Sometimes there may be clues, such as when a bottle that had just been thrown can be traced back to an outstretched arm.  But things are not always straightforward.

For example, say you observe a bottle mid-way between the parties.  The arm that threw it has been retracted so there’s no information about where it came from or which direction it is moving.  We’ll also say this situation is somehow taking place in a vacuum so as to remove any evidence of air compression surrounding the bottle.  (after all, all great physics experiments take place in vacuums!)

So you decide to solve the puzzle using other means.  Taking out some scientific equipment such as microscopes, interferometers, etc., you set to work.  But after studying it for an hour (in your time) you remain perplexed.  There appears to be no information that would allow you to make a decision.  Every atom and every subatomic particle within the bottle is stone cold.  Yet you know the bottle must be moving because it can’t float at that position.

At this point you give up and decide to advance universal time by one tenth of a second.  Having done so you notice the bottle is now located slightly to the left of where it was previously.  Aha!  So now you know which way it is moving.

But hold on a second.  How did the bottle ‘know’ where to relocate itself?

In science there is a principle called Cause & Effect (C&E).  What it says is that the information contained in a situation in any point in time fully determines the situation at a later point in time.

We often think of C&E in terms of interactions; such as if I hit an egg with a hammer, the egg will break.  In this case the hammer-striking-the-egg is the Cause and the egg-breaking is the Effect.  But the principle also applies to simpler situations.  For example, take a stone moving through space: in the absence of any force, the position and velocity of the stone at one point in time will fully determine its position at any future time.

Back to the bottle.  While examining it frozen in time you could find no information about which direction it was moving.  Yet a short while later it had relocated itself.  That means, according to C&E, the information about which direction it was moving and how fast it was moving must somehow be contained within the situation that was frozen in time.  If this was not the case the bottle couldn't move.  The same must also be said of every atom and every subatomic particle within the bottle.  Each of them must ‘have knowledge’ about their velocity in order to change positions from one moment to the next.  That is, the velocity must be ‘stored’ within each particle; otherwise the principle of C&E falls apart.

What this tells us is that velocity is a property of matter rather than simply a measure of how far something travels in a unit duration of time.

The only other possibility is that each particle contains knowledge of its current position and its historical position a ‘short while’ ago, in order to calculate velocity.  For reasons described later, the storing of position won’t be possible.  But putting that aside, the idea that a particle could store historical information is even less plausible.  Hence the most likely explanation is that it stores velocity.

Some might ask, how can velocity be stored within matter?  One might just as well ask how mass and charge could be stored within matter.  The point is, we don’t know how either of these things are stored but we do accept they are stored somehow.

The difference here is that velocity is a variable rather than static quantity.  But making a quantity variable doesn’t violate physics laws.  For example if the mass of an electron varied with time, the only effect would be that its acceleration would also vary with time when exposed to a constant force.  Since variable accelerations are allowed, variable masses are not forbidden.  The same argument can then be made in regards to charge and velocity.

Zeno’s Arrow Paradox

The above scenario has a precursor in an ancient riddle known as Zeno’s Arrow Parodox.  It goes like this (somewhat reworded):

An archer has two arrows.  He places one on the ground and fires the other across a field.  Once the fired arrow has left the bow, why does it continue to move while the other stays motionless?

A close examination of both arrows before and after reveals them to be identical in every perceivable way.  And if someone were to run alongside the fired arrow while it was in motion, he would notice no difference between that and the other.  That being the case, why should one continue to change its location while the other doesn't?

An objection to this would be that, depending on our frame of reference, either arrow could be considered as moving.  And so the question of why one moves rather than the other comes down to semantics.  A fair point.  So let’s modify the situation.

This time there are three arrows (A,B,C) and two archers.  Arrow A stays ‘motionless’ on the ground, and arrows B and C are fired simultaneously in opposite directions.  The question now becomes: why does the distance between B and C enlarge more quickly than the distance between B and A?

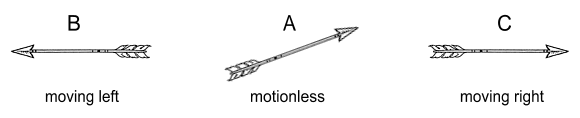
Notice the question no longer depends on frames of reference or descriptions of ‘moving’ versus ‘still’, because we are looking at rates at which distances enlarge, and these will enlarge in the same manner regardless of our reference point.

For example, if we take arrow B as our reference point, we notice arrow C moves away (changes its location) at double the rate of arrow A.  But if both A and C are physically identical, and everything that surrounds them is identical, why would they update their locations in different manner (relative to B)?  Something about them must be different.

One undeniable difference between the fired and grounded arrows is that the fired arrows experienced a force.  This caused them to accelerate to a certain speed.  But once that force ceased, what now is the difference?  Do the arrows retain a memory of the accumulated forces applied to them?  If so they would have need to retain an infinite memory because forces can accumulate over very long periods.  In fact it can be argued that every subatomic particle in the universe has its present location due to all the forces that were applied to it over its lifetime, and this could be unlimited in duration.

So yes, perhaps each ‘particle of matter’ retains a record of all the forces that have ever been applied to it.  But a much simpler proposal is that it carries only ‘knowledge’ of its current velocity.

Relative or Absolute?

If we take it as confirmed (by logical extension of C&E) that velocity is stored within matter, another interesting fact follows.  Up to now we are still talking about velocity as being relative.  However if velocity is to be a property of substance there is no way it could be stored as a relative quantity.  Because if velocity was stored as a relative quantity it would require each particle store multiple values of velocity – one for every other particle in existence – and that every particle be instantaneously aware of the movements of all others.  Clearly neither of these postulates can be acceptable.

This leads to the conclusion that velocity is stored within matter as an absolute rather than relative quantity.

Obvious questions arise from this.  The first one being: what are these velocities with respect to?  The short answer being: not to anything.  At least not to anything physical.  And nor would they need to be.  That’s the whole point of ‘absolute’ after all.

Occasionally a particle might have an absolute velocity of zero.  However the occurrence will only be temporary and accidental because particles experience force and change velocities all the time.  So again, a particle requires no reference points or ‘frames’ to measure its velocity against, just as it requires no reference masses or charges.

Can Absolute Velocities be Measured?

Another question that follows is, is it possible to measure or even detect a particle’s absolute velocity?  The answer is: probably not.  All physical laws appear to be based entirely on velocity differences between particles.  So while all particles will have an absolute velocity there may not be any experiments capable of detecting what those velocities are.

For example suppose we have three particles: the first one described as being ‘at rest’, the second moving away from the first at 1 m/s and the third moving toward the first at 2 m/s.  The actual absolute velocities of these might respectively be 50,634,821 m/s, 50,634,822 m/s, and 50,634,819 m/s.  Naturally these numbers are purely made up.  But the point here is that when these particles come together and interact, any forces between them will be based only on the differences between such velocities. Hence we will be unable to detect their absolute velocities.

Velocity directions

Of course there is more to velocity than its magnitude or speed.  Velocities also have direction.  That is, velocity is a vectored quantity.  Therefore if matter is to store information that describes its velocity it must also store information describing its direction.  In a three-dimensional world this requires three numbers which are described by a coordinate system.  There are several such systems to choose from.  One is the cartesian, which describes X, Y, and Z.  Another is the spherical, which describes a magnitude (R) and two latitude/longitude angles (θ and φ).  Another again is the cylindrical coordinate system.

In fact there are any number of coordinate systems we could invent to describe a velocity in three dimensions.  The most likely however of these is the cartesian system because it is the simplest and all the units (X,Y,Z) are equivalent in describing the same property.  Storing information in terms of another coordinate system, such as spherical coordinates, will lead to other problems which are too complex to delve into here.

If we take it that each particle of matter contains three pieces of data that describe its velocity, such as X, Y and Z components, a further requirement follows from this.  Namely that the cosmos, i.e. the empty space containing the physical universe, must have a fixed set of directions that velocities are described against.  That is there must be a certain fixed direction that describes the ‘X’ component of velocity and likewise with Y and Z.  This requirement would also hold true for any other coordinate system.

This is not to say that we can detect such absolute directions because the interaction between matter gives out no such clues.  We can only know the requirement for their existence follows from the requirement of storing velocities.

What about Position?

The third question that follows is, are there such things as absolute positions/locations and does matter store information about its location?  The answer to both is: most likely not.

There are two reasons for saying this.  Firstly, as pointed in the cosmology chapter, the size of physical space must be infinitely large in all directions.  This would mean that, if the cosmos did have central point, such as a location with coordinates (0,0,0), the bulk of the cosmos would be infinitely far away from it.  Thus if matter were to store its absolute position it would need to store infinite values.  This will not be possible.  The same issue will not be a problem for velocity because a particle can never gain an infinite velocity.  This is because particles can only receive finite forces, which lead to finite accelerations and hence finite velocities.

The second reason why matter does not need to store position is that no physical interaction laws are based on it.  That is, no calculation of force is based on the distance between two objects.

This claim might sound remarkable because distance features prominently in many force equations.  For example both the electrical force law (Coulomb’s) and the gravitational force law (Newton’s) contain a distance-squared term in the denominator.  Thus it would seem the force between charged or massive objects is directly dependent on the distance between them.  Surprisingly however, this is not the case.

To demonstrate this, consider two like-charged particles such as electrons.  We will call one the ‘source’ and the other the ‘target’.  The force the target feels is calculated by multiplying the magnitude of both charges and dividing by the square of the distance between them.  This would appear to make the force a function of distance.  In reality though, the target doesn’t know anything about the source.  The only thing it feels is the field coming from it.  That field could have instead come from multiple charges located at a variety of distances.  Coulomb’s law is simply a way of determining how the field strength of a point charge weakens as it expands uniformly across a spherical surface in three dimensions.  The same argument can be made in regards to gravitational forces.  That is, a target mass responds to a local gravity-field strength rather than to a distance from a source mass.

Conclusions

The principle of Cause & Effect requires that the universe must contain all the information at a given instant of time that would allow its situation to be determined at a later point in time.  It necessarily follows from this that velocity must be stored within matter, as a property of matter.  It also follows that this velocity be an absolute rather than a relative quantity and that it be stored as three components corresponding to each of the dimensions.  There is possibly no way of detecting or measuring this absolute velocity since all physical reactions (forces) are based on differences between such velocities.  The same conclusions cannot be said about distances, or rather, positions.  That is, position is not stored within matter and the concept of absolute positions likely has no meaning.